DDIA: Chapter 9 Consistency and Consensus

本章是这本书最酣畅淋漓的一章，涉及到了一致性和共识问题的方方面面，知识点多而不失条理。第一部分先讲了 Linearizability, 为后面的知识点做铺垫。到了 “Ordering Guarantees” 这一小节，从因果关系的带来的 “Happened Before” 的关系开始讲起，讲到了序列号和 Lamport Timestamp，提出来 Lamport Timestamp 的一个缺点：无法在某事件发生时判断是否有冲突，然后引出了全序关系广播，在全序关系广播中又讲到了和 Linearizable 之间的等价关系，最后引出共识算法。太精彩了，值得反复阅读！

Consistency Guarantees

Most replicated databases provide at least eventual consistency, which means that if you stop writing to the database and wait for some unspecified length of time, then eventually all read requests will return the same value.

A better name for eventual consistency may be convergence, as we expect all replicas to eventually converge to the same value.

convergence，直接译为收敛感觉最为形象，引用数学里的意思：随着某个值的变化，某个东西的状态最终趋于一个特定值。

Systems with stronger guarantees may have worse performance or be less fault-tolerant than systems with weaker guarantees. Nevertheless, stronger guarantees can be appealing because they are easier to use correctly.

Linearizability

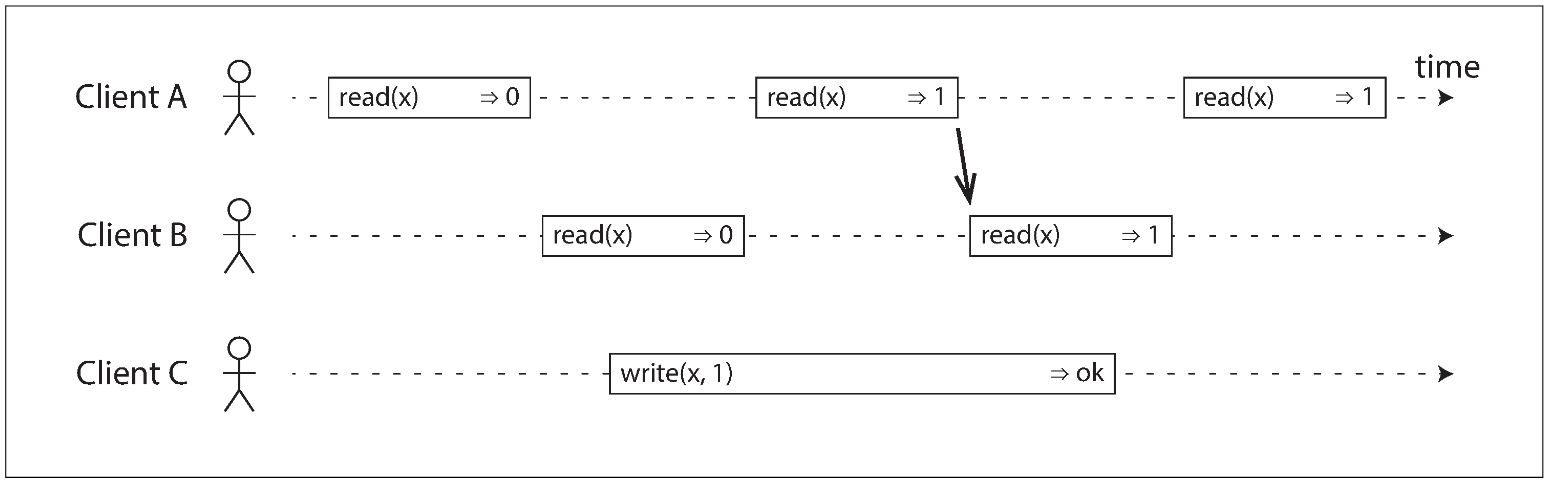
In a linearizable system, as soon as one client successfully completes a write, all clients reading from the database must be able to see the value just written. Maintaining the illusion of a single copy of the data means guaranteeing that the value read is the most recent, up-to-date value, and doesn’t come from a stale cache or replica.

In other words, linearizability is a recency guarantee.

What Makes a System Linearizable?

The basic idea behind linearizability is simple: to make a system appear as if there is only a single copy of the data.

Linearizability Versus Serializability

• Serializability
  • Serializability is an isolation property of transactions, where every transaction may read and write multiple objects.
  • It guarantees that transactions behave the same as if they had executed in some serial order.
  • It is okay for that serial order to be different from the order in which transactions were actually run.
• Linearizability
  • Linearizability is a recency guarantee on reads and writes of a register.
  • It doesn’t group operations together into transactions, so it does not prevent problems such as write skew.

A database may provide both serializability and linearizability, and this combination is known as strict serializability or strong one-copy serializability.

Implementations of serializability based on two-phase locking or actual serial execution are typically linearizable.

Relying on Linearizability

Locking and Leader election

A system that uses single-leader replication needs to ensure that there is indeed only one leader, not several. One way of electing a leader is to use a lock: every node that starts up tries to acquire the lock, and the one that succeeds becomes the leader.

No matter how this lock is implemented, it must be linearizable: all nodes must agree which node owns the lock; otherwise it is useless.

Coordination services like Apache ZooKeeper and etcd are often used to implement distributed locks and leader election. They use consensus algorithms to implement linearizable operations in a fault-tolerant way.

严格意义上来说， ZooKeeper 和 etcd 都只提供线性写，即可能会读到旧数据，但是你可以请求一个线性读的操作：

• etcd calls this a quorum read
• in ZooKeeper you need to call sync()

Constraints and uniqueness guarantees

Uniqueness constraints are common in databases: for example, a username or email address must uniquely identify one user, and in a file storage service there cannot be two files with the same path and filename.

If you want to enforce this constraint as the data is written (such that if two people try to concurrently create a user or a file with the same name, one of them will be returned an error), you need linearizability.

This situation is actually similar to a lock: when a user registers for your service, you can think of them acquiring a “lock” on their chosen username.

Cross-channel timing dependencies

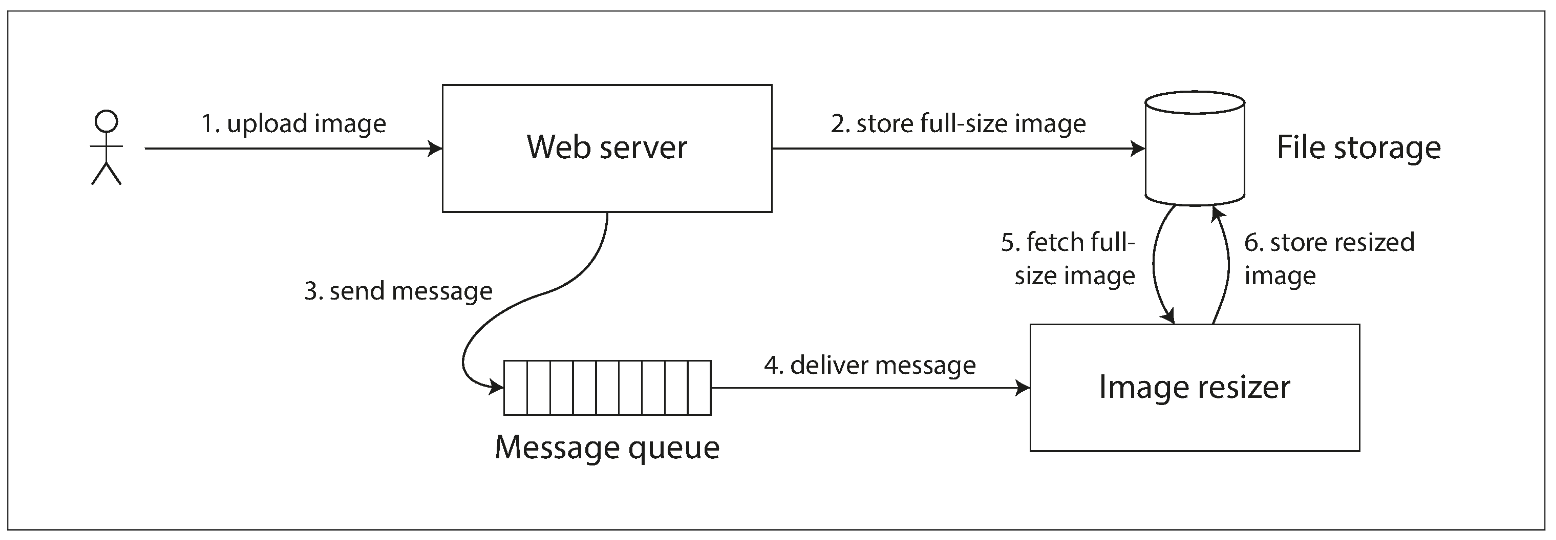
If the file storage service is linearizable, then this system should work fine. If it is not linearizable, there is the risk of a race condition: the message queue (steps 3 and 4) might be faster than the internal replication inside the storage service. In this case, when the resizer fetches the image (step 5), it might see an old version of the image, or nothing at all. If it processes an old version of the image, the full-size and resized images in the file storage become permanently inconsistent.

This problem arises because there are two different communication channels between the web server and the resizer: the file storage and the message queue. Without the recency guarantee of linearizability, race conditions between these two channels are possible.

Implementing Linearizable Systems

The most common approach to making a system fault-tolerant is to use replication. Let’s revisit the replication methods and compare whether they can be made linearizable:

• Single-leader replication (potentially linearizable)
  • In a system with single-leader replication, the leader has the primary copy of the data that is used for writes, if you make reads from the leader, or from synchronously updated followers, they have the potential to be linearizable.
• Multi-leader replication (not linearizable)
  • Systems with multi-leader replication are generally not linearizable, because they concurrently process writes on multiple nodes and asynchronously replicate them to other nodes.
• Leaderless replication (probably not linearizable)
  • People sometimes claim that you can obtain “strong consistency” by requiring quorum reads and writes (w + r > n).
  • Depending on the exact configuration of the quorums, and depending on how you define strong consistency, this is not quite true.
• Consensus algorithms (linearizable)
  • Some consensus algorithms bear a resemblance to single-leader replication. However, consensus protocols contain measures to prevent split brain and stale replicas.

Linearizability and quorums

Intuitively, it seems as though strict quorum reads and writes should be linearizable in a Dynamo-style model. However, when we have variable network delays, it is possible to have race conditions, as demonstrated below:

The initial value of x is 0, and a writer client is updating x to 1 by sending the write to all three replicas (n = 3, w = 3). Concurrently, client A reads from a quorum of two nodes (r = 2) and sees the new value 1 on one of the nodes. Also concurrently with the write, client B reads from a different quorum of two nodes, and gets back the old value 0 from both.

This execution is nevertheless not linearizable: B’s request begins after A’s request completes, but B returns the old value while A returns the new value.

Interestingly, it is possible to make Dynamo-style quorums linearizable at the cost of reduced performance:

• A reader must perform read repair synchronously, before returning results to the application.
• A writer must read the latest state of a quorum of nodes before sending its writes. Moreover, only linearizable read and write operations can be implemented in this way; a linearizable compare-and-set operation cannot, because it requires a consensus algorithm.

The Cost of Linearizability

The CAP theorem

The trade-off is as follows:

• If your application requires linearizability, and some replicas are disconnected from the other replicas due to a network problem, then some replicas cannot process requests while they are disconnected: they must either wait until the network problem is fixed, or return an error (either way, they become unavailable).
• If your application does not require linearizability, then it can be written in a way that each replica can process requests independently, even if it is disconnected from other replicas (e.g., multi-leader). In this case, the application can remain available in the face of a network problem, but its behavior is not linearizable.

Thus, a better way of phrasing CAP would be either Consistent or Available when Partitioned.

The CAP theorem as formally defined is of very narrow scope: it only considers one consistency model (namely linearizability) and one kind of fault (network partitions, vi or nodes that are alive but disconnected from each other). It doesn’t say anything about network delays, dead nodes, or other trade-offs.

Thus, although CAP has been historically influential, it has little practical value for designing systems.

Linearizability and network delays

Although linearizability is a useful guarantee, surprisingly few systems are actually linearizable in practice.

If you want linearizability, the response time of read and write requests is at least proportional to the uncertainty of delays in the network.

A faster algorithm for linearizability does not exist, but weaker consistency models can be much faster, so this trade-off is important for latency-sensitive systems.

Ordering Guarantees

Something about ordering:

• the main purpose of the leader in single-leader replication is to determine the order of writes in the replication log—that is, the order in which followers apply those writes. If there is no single leader, conflicts can occur due to concurrent operations.
• Serializability, is about ensuring that transactions behave as if they were executed in some sequential order.
• The use of timestamps and clocks in distributed systems is another attempt to introduce order into a disorderly world, for example to determine which one of two writes happened later.

Ordering and Causality

There are several reasons why ordering keeps coming up, and one of the reasons is that it helps preserve causality.

Causality imposes an ordering on events: cause comes before effect; a message is sent before that message is received; the question comes before the answer.

If a system obeys the ordering imposed by causality, we say that it is causally consistent.

The Causal order is not a total order

A total order allows any two elements to be compared, so if you have two elements, you can always say which one is greater and which one is smaller.

The difference between a total order and a partial order is reflected in different database consistency models:

• Linearizability
  • In a linearizable system, we have a total order of operations: if the system behaves as if there is only a single copy of the data, and every operation is atomic, this means that for any two operations we can always say which one happened first.
• Causality
  • We said that two operations are concurrent if neither happened before the other. Two events are ordered if they are causally related (one happened before the other), but they are incomparable if they are concurrent. This means that causality defines a partial order, not a total order: some operations are ordered with respect to each other, but some are incomparable.

Therefore, according to this definition, there are no concurrent operations in a linearizable datastore: there must be a single timeline along which all operations are totally ordered.

Concurrency would mean that the timeline branches and merges again—and in this case, operations on different branches are incomparable.

Linearizability is stronger than causal consistency

So what is the relationship between the causal order and linearizability? The answer is that linearizability implies causality: any system that is linearizable will preserve causality correctly.

The good news is that a middle ground is possible. Linearizability is not the only way of preserving causality—there are other ways too. A system can be causally consistent without incurring the performance hit of making it linearizable.

In fact, causal consistency is the strongest possible consistency model that does not slow down due to network delays, and remains available in the face of network failures.

Sequence Number Ordering

However, there is a better way: we can use sequence numbers or timestamps to order events. A timestamp need not come from a time-of-day clock. It can instead come from a logical clock, which is an algorithm to generate a sequence of numbers to identify operations, typically using counters that are incremented for every operation.

Such sequence numbers or timestamps are compact, and they provide a total order.

只要我们获得了所有事件的全局排序，那么各种一致性模型对于读写操作所呈现的排序要求，很自然就能得到满足。

In particular, we can create sequence numbers in a total order that is consistent with causality: we promise that if operation A causally happened before B, then A occurs before B in the total order (A has a lower sequence number than B).

Concurrent operations may be ordered arbitrarily.

Such a total order captures all the causality information, but also imposes more ordering than strictly required by causality.

In a database with single-leader replication, the replication log defines a total order of write operations that is consistent with causality.

Non-causal sequence number generators

If there is not a single leader (perhaps because you are using a multi-leader or leaderless database, or because the database is partitioned), it is less clear how to generate sequence numbers for operations. Various methods are used in practice:

• Each node can generate its own independent set of sequence numbers. For example, if you have two nodes, one node can generate only odd numbers and the other only even numbers.
• You can attach a timestamp from a time-of-day clock (physical clock) to each operation. Such timestamps are not sequential, but if they have sufficiently high resolution, they might be sufficient to totally order operations.
• You can preallocate blocks of sequence numbers.

These three options all perform better and are more scalable than pushing all operations through a single leader that increments a counter.

However, they all have a problem: the sequence numbers they generate are not consistent with causality.

Lamport timestamps

通过说明分布式下序列号生成失去了因果关系的一致性，引出了一种新的解决方法：Lamport Timestamp.

Although the three sequence number generators just described are inconsistent with causality, there is actually a simple method for generating sequence numbers that is consistent with causality. It is called a Lamport timestamp(“time, clocks, and the ordering of event in the distributed systems”).

Each node has a unique identifier, and each node keeps a counter of the number of operations it has processed. The Lamport timestamp is then simply a pair of (counter, node ID).

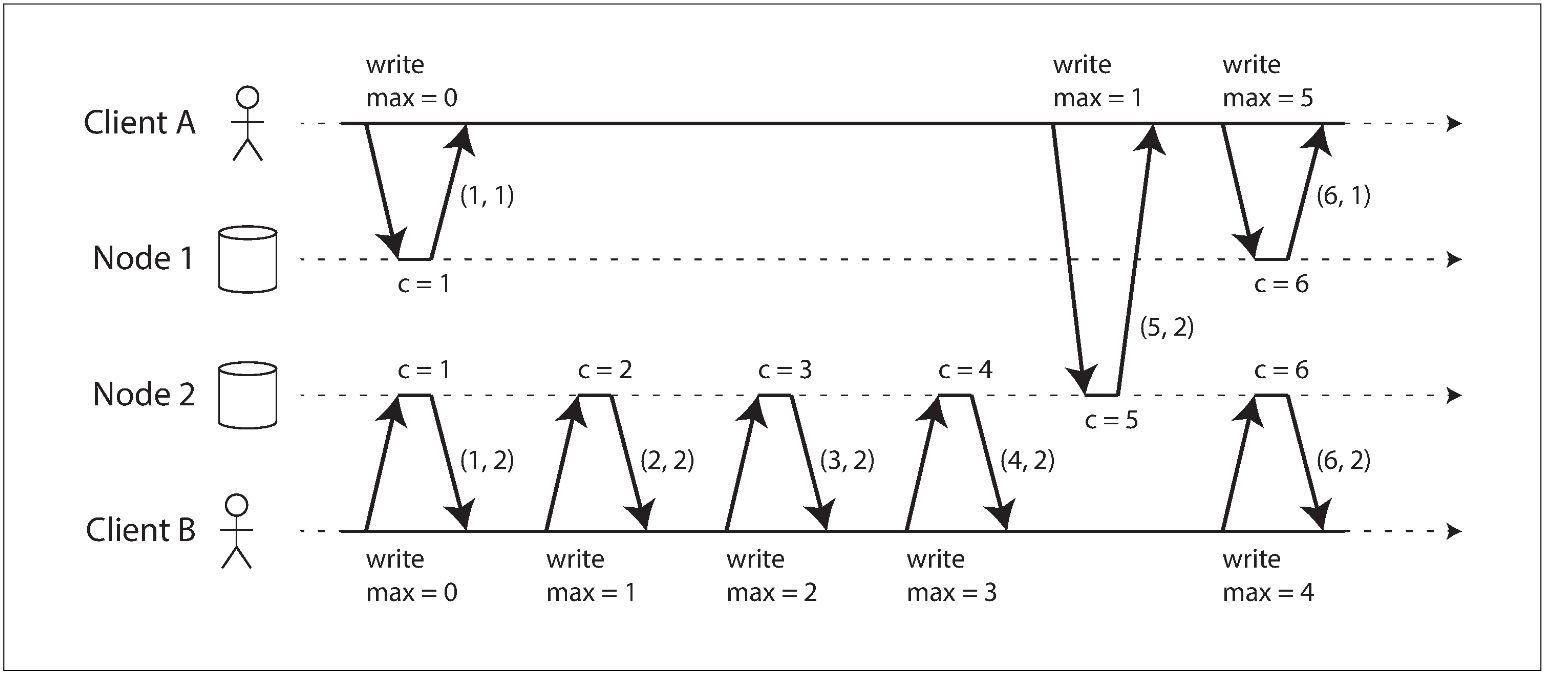
A Lamport timestamp bears no relationship to a physical time-of-day clock, but it provides total ordering: if you have two timestamps, the one with a greater counter value is the greater timestamp; if the counter values are the same, the one with the greater node ID is the greater timestamp.

The key idea about Lamport timestamps, which makes them consistent with causality, is the following: every node and every client keeps track of the maximum counter value it has seen so far, and includes that maximum on every request.

When a node receives a request or response with a maximum counter value greater than its own counter value, it immediately increases its own counter to that maximum.

As long as the maximum counter value is carried along with every operation, this scheme ensures that the ordering from the Lamport timestamps is consistent with causality, because every causal dependency results in an increased timestamp.

直观一点解释，因果性体现在哪些方面：

• 同一个进程内部的前后两个操作可能具有因果性：
  • Lamport Timestamp 保证了后进行的操作时间戳一定比前面进行的操作大。
• 不同进程之间，消息的发送方和消息的接收方可能具有因果性：
  • Lamport Timestamp 保证了消息的接收方的时间戳一定比消息发送方的时间戳大。

Timestamp ordering is not sufficient

“很有启发的一集。”

Although Lamport timestamps define a total order of operations that is consistent with causality, they are not quite sufficient to solve many common problems in distributed systems.

For example, consider a system that needs to ensure that a username uniquely identifies a user account. If two users concurrently try to create an account with the same username, one of the two should succeed and the other should fail.

At first glance, it seems as though a total ordering of operations (e.g., using Lamport timestamps) should be sufficient to solve this problem: if two accounts with the same username are created, pick the one with the lower timestamp as the winner (the one who grabbed the username first), and let the one with the greater timestamp fail. Since timestamps are totally ordered, this comparison is always valid.

This approach works for determining the winner after the fact: once you have collected all the username creation operations in the system, you can compare their timestamps. However, it is not sufficient when a node has just received a request from a user to create a username, and needs to decide right now whether the request should succeed or fail.

The problem here is that the total order of operations only emerges after you have collected all of the operations. If another node has generated some operations, but you don’t yet know what they are, you cannot construct the final ordering of operations.

To conclude: in order to implement something like a uniqueness constraint for usernames, it’s not sufficient to have a total ordering of operations — you also need to know when that order is finalized.

If you have an operation to create a username, and you are sure that no other node can insert a claim for the same username ahead of your operation in the total order, then you can safely declare the operation successful. This idea of knowing when your total order is finalized is captured in the topic of total order broadcast.

Total Order Broadcast

As discussed, single-leader replication determines a total order of operations by choosing one node as the leader and sequencing all operations on a single CPU core on the leader.

The challenge then is how to scale the system if the throughput is greater than a single leader can handle, and also how to handle failover if the leader fails. In the distributed systems literature, this problem is known as total order broadcast or atomic broadcast.

很多时候系统里的全序关系都是由 single-leader 维护的，因为所有的读和写请求都由它处理，最后写入日志的顺序就是整个系统中的全序顺序。但是如果系统的吞吐量大于了单个节点能够处理的范围或者当前的 Leader 挂掉了，全序关系广播就能发挥作用了。

Total order broadcast is usually described as a protocol for exchanging messages between nodes. Informally, it requires that two safety properties always be satisfied:

• Reliable delivery
  • No messages are lost: if a message is delivered to one node, it is delivered to all nodes.
• Totally ordered delivery
  • Messages are delivered to every node in the same order.

Using total order broadcast

Consensus services such as ZooKeeper and etcd actually implement total order broadcast.

This fact is a hint that there is a strong connection between total order broadcast and consensus.

Total order broadcast is exactly what you need for database replication: if every message represents a write to the database, and every replica processes the same writes in the same order, then the replicas will remain consistent with each other (aside from any temporary replication lag). This principle is known as state machine replication.

An important aspect of total order broadcast is that the order is fixed at the time the messages are delivered: a node is not allowed to retroactively insert a message into an earlier position in the order if subsequent messages have already been delivered. This fact makes total order broadcast stronger than timestamp ordering.

Another way of looking at total order broadcast is that it is a way of creating a log (as in a replication log, transaction log, or write-ahead log): delivering a message is like appending to the log. Since all nodes must deliver the same messages in the same order, all nodes can read the log and see the same sequence of messages.

Implementing linearizable storage using total order broadcast

注意这节的小标题是用 total order broadcast 实现一个 linearizable storage.

Total order broadcast is asynchronous: messages are guaranteed to be delivered reliably in a fixed order, but there is no guarantee about when a message will be delivered (so one recipient may lag behind the others). By contrast, linearizability is a recency guarantee: a read is guaranteed to see the latest value written.

所以如何解决前文提到的那个用户名限制的问题呢？

Imagine that for every possible username, you can have a linearizable register with an atomic compare-and-set operation.

Every register initially has the value null (indicating that the username is not taken). When a user wants to create a username, you execute a compare-and-set operation on the register for that username, setting it to the user account ID, under the condition that the previous register value is null. If multiple users try to concurrently grab the same username, only one of the compare-and-set operations will succeed, because the others will see a value other than null (due to linearizability).

为什么 compare-and-set 机制需要 linearizability 呢？

你可以这么想：compare-and-set 操作是有 recency 需求的，即必须保证每次 compare 操作都一定能读到最新的数据，然而只有 linearizability 才能提供这种 recency guarantee。

You can implement such a linearizable compare-and-set operation as follows by using total order broadcast as an append-only log:

1. Append a message to the log, tentatively indicating the username you want to claim.
2. Read the log, and wait for the message you appended to be delivered back to you.
3. Check for any messages claiming the username that you want.

• If the first message for your desired username is your own message, then you are successful: you can commit the username claim (perhaps by appending another message to the log) and acknowledge it to the client.
• If the first message for your desired username is from another user, you abort the operation.

A similar approach can be used to implement serializable multi-object transactions on top of a log.

While this procedure ensures linearizable writes, it doesn’t guarantee linearizable reads — if you read from a store that is asynchronously updated from the log, it may be stale. (To be precise, the procedure described here provides sequential consistency, sometimes also known as timeline consistency, a slightly weaker guarantee than linearizability.) To make reads linearizable, there are a few options:

• You can sequence reads through the log by appending a message, reading the log, and performing the actual read when the message is delivered back to you.
  • etcd somehow works like this.
• If the log allows you to fetch the position of the latest log message in a linearizable way, you can query that position, wait for all entries up to that position to be delivered to you, and then perform the read.
  • This is the idea behind ZooKeeper’s sync() operation.
• You can make your read from a replica that is synchronously updated on writes, and is thus sure to be up to date.
  • This technique is used in chain replication.

Implementing total order broadcast using linearizable storage

用 linearizable storage 实现一个 total order broadcast

The easiest way is to assume you have a linearizable register that stores an integer and that has an atomic increment-and-get operation. Alternatively, an atomic compare-and-set operation would also do the job.

The algorithm is simple:

• For every message you want to send through total order broadcast, you increment-and-get the linearizable integer
• Attach the value you got from the register as a sequence number to the message.
• You can then send the message to all nodes (resending any lost messages), and the recipients will deliver the messages consecutively by sequence number.

Note that unlike Lamport timestamps, the numbers you get from incrementing the linearizable register form a sequence with no gaps. Thus, if a node has delivered message 4 and receives an incoming message with a sequence number of 6, it knows that it must wait for message 5 before it can deliver message 6.

这里结合 linearizable storage 来说明一下如何利用全序关系广播来维护唯一性限制的，用注册用户名来说明：

首先分为上层应用和下层协议：

1. 用户在输入用户名后，上层应用向下层协议提出消息。
2. 上层应用监视下层协议的消息提交，如果第一条有关某用户名的声称是自己提交的，那么该用户名可用，否则已经被占用。
3. 下层协议收到消息后，向 linearizable storage 执行 increment-and-get 操作获取序列号。
4. 获取序列号后，下层协议先向自己的上层应用提交该消息，再向其他所有节点广播该消息。

步骤 3 是需要时间的，如果上层应用在提出消息后还没收到自己的消息时，收到了来自于其他节点的关于相同用户名的声称，则知晓该用户名已经被占用。

This is the key difference between total order broadcast and timestamp ordering.

How hard could it be to make a linearizable integer with an atomic increment-and-get operation?

As usual, if things never failed, it would be easy: you could just keep it in a variable on one node. The problem lies in handling the situation when network connections to that node are interrupted, and restoring the value when that node fails.

In general, if you think hard enough about linearizable sequence number generators, you inevitably end up with a consensus algorithm.

This is no coincidence: it can be proved that a linearizable compare-and-set (or increment-and-get) register and total order broadcast are both equivalent to consensus. That is, if you can solve one of these problems, you can transform it into a solution for the others.

This is quite a profound and surprising insight!

Distributed Transactions and Consensus

Consensus is one of the most important and fundamental problems in distributed computing. On the surface, it seems simple: informally, the goal is simply to get several nodes to agree on something.

Atomic Commit and Two-Phase Commit (2 PC)

Introduction to two-phase commit

Two-phase commit is an algorithm for achieving atomic transaction commit across multiple nodes—i.e., to ensure that either all nodes commit or all nodes abort.

A system of promises

In a bit more detail:

1. When the application wants to begin a distributed transaction, it requests a transaction ID from the coordinator. This transaction ID is globally unique.
2. The application begins a single-node transaction on each of the participants, and attaches the globally unique transaction ID to the single-node transaction. All reads and writes are done in one of these single-node transactions.
3. When the application is ready to commit, the coordinator sends a prepare request to all participants, tagged with the global transaction ID.
4. When a participant receives the prepare request, it makes sure that it can definitely commit the transaction under all circumstances.
5. When the coordinator has received responses to all prepare requests, it makes a definitive decision on whether to commit or abort the transaction.
6. Once the coordinator’s decision has been written to disk, the commit or abort request is sent to all participants. If this request fails or times out, the coordinator must retry forever until it succeeds.

Thus, the protocol contains two crucial “points of no return”:

1. When a participant votes “yes,” it promises that it will definitely be able to commit later (although the coordinator may still choose to abort).
2. Once the coordinator decides, that decision is irrevocable. Those promises ensure the atomicity of 2 PC.

Distributed Transactions in Practice

Some implementations of distributed transactions carry a heavy performance penalty —for example, distributed transactions in MySQL are reported to be over 10 times slower than single-node transactions.

Two quite different types of distributed transactions are often conflated:

• Database-internal distributed transactions
  • Some distributed databases (i.e., databases that use replication and partitioning in their standard configuration) support internal transactions among the nodes of that database.
  • In this case, all the nodes participating in the transaction are running the same database software.
• Heterogeneous distributed transactions
  • In a heterogeneous transaction, the participants are two or more different technologies: for example, two databases from different vendors, or even non-database systems such as message brokers.

Limitations of distributed transactions

XA transactions solve the real and important problem of keeping several participant data systems consistent with each other, but as we have seen, they also introduce major operational problems. In particular, the key realization is that the transaction coordinator is itself a kind of database:

• If the coordinator is not replicated but runs only on a single machine, it is a single point of failure for the entire system.
• Many server-side applications are developed in a stateless model (as favored by HTTP), with all persistent state stored in a database.
• Since XA needs to be compatible with a wide range of data systems, it is necessarily a lowest common denominator.

Fault-Tolerant Consensus

The consensus problem is normally formalized as follows: one or more nodes may propose values, and the consensus algorithm decides on one of those values.

In this formalism, a consensus algorithm must satisfy the following properties:

• Uniform agreement
  • No two nodes decide differently.
• Integrity
  • No node decides twice.
• Validity
  • If a node decides value v, then v was proposed by some node.
• Termination
  • Every node that does not crash eventually decides some value.
  • This is a liveness property.
  • In particular, 2PC does not meet the requirements for termination.

The uniform agreement and integrity properties define the core idea of consensus: everyone decides on the same outcome, and once you have decided, you cannot change your mind.

Consensus algorithms and total order broadcast

The best-known fault-tolerant consensus algorithms are Viewstamped Replication (VSR), Paxos, Raft, and Zab. There are quite a few similarities between these algorithms, but they are not the same.

Remember that total order broadcast requires messages to be delivered exactly once, in the same order, to all nodes. If you think about it, this is equivalent to performing several rounds of consensus: in each round, nodes propose the message that they want to send next, and then decide on the next message to be delivered in the total order.

So, total order broadcast is equivalent to repeated rounds of consensus (each consensus decision corresponding to one message delivery):

• Due to the agreement property of consensus, all nodes decide to deliver the same messages in the same order.
• Due to the integrity property, messages are not duplicated.
• Due to the validity property, messages are not corrupted and not fabricated out of thin air.
• Due to the termination property, messages are not lost.

Viewstamped Replication, Raft, and Zab implement total order broadcast directly, because that is more efficient than doing repeated rounds of one-value-at-a-time consensus. In the case of Paxos, this optimization is known as Multi-Paxos.

Single-leader replication and consensus

粗看本章的内容，好像第 5 章讲到的 single-leader replication 已经是个全序关系广播了：it takes all the writes to the leader and applies them to the followers in the same order, thus keeping replicas up to date.

作者在这个小节回答了这个疑问。

The answer comes down to how the leader is chosen. If the leader is manually chosen and configured by the humans in your operations team, you essentially have a “consensus algorithm” of the dictatorial variety: only one node is allowed to accept writes (i.e., make decisions about the order of writes in the replication log), and if that node goes down, the system becomes unavailable for writes until the operators manually configure a different node to be the leader. Such a system can work well in practice, but it does not satisfy the termination property of consensus because it requires human intervention in order to make progress.

Some databases perform automatic leader election and failover, promoting a follower to be the new leader if the old leader fails. This brings us closer to fault-tolerant total order broadcast, and thus to solving consensus.

However, there is a problem. We previously discussed the problem of split brain, and said that all nodes need to agree who the leader is—otherwise two different nodes could each believe themselves to be the leader, and consequently get the database into an inconsistent state. Thus, we need consensus in order to elect a leader. But if the consensus algorithms described here are actually total order broadcast algorithms, and total order broadcast is like single-leader replication, and single-leader replication requires a leader, then…

It seems that in order to elect a leader, we first need a leader. In order to solve consensus, we must first solve consensus. How do we break out of this conundrum?

Epoch numbering and quorums

All of the consensus protocols discussed so far internally use a leader in some form or another, but they don’t guarantee that the leader is unique. Instead, they can make a weaker guarantee: the protocols define an epoch number (called the ballot number in Paxos, view number in Viewstamped Replication, and term number in Raft) and guarantee that within each epoch, the leader is unique.

Thus, we have two rounds of voting: once to choose a leader, and a second time to vote on a leader’s proposal. The key insight is that the quorums for those two votes must overlap.

Limitations of consensus

The benefits of consensus algorithm come at a cost:

• The process by which nodes vote on proposals before they are decided is a kind of synchronous replication.
• Consensus systems always require a strict majority to operate. This means you need a minimum of three nodes in order to tolerate one failure.
• Consensus systems generally rely on timeouts to detect failed nodes. Frequent leader elections result in terrible performance because the system can end up spending more time choosing a leader than doing any useful work.
• Sometimes, consensus algorithms are particularly sensitive to network problems.

Membership and Coordination Services

As an application developer, you will rarely need to use ZooKeeper directly, because it is actually not well suited as a general-purpose database. It is more likely that you will end up relying on it indirectly via some other project: for example, HBase, Hadoop YARN, OpenStack Nova, and Kafka all rely on ZooKeeper running in the background.

ZooKeeper and etcd are designed to hold small amounts of data that can fit entirely in memory. That small amount of data is replicated across all the nodes using a fault-tolerant total order broadcast algorithm.

Total order broadcast is just what you need for database replication: if each message represents a write to the database, applying the same writes in the same order keeps replicas consistent with each other.

ZooKeeper is modeled after Google’s Chubby lock service, implementing not only total order broadcast (and hence consensus), but also an interesting set of other features that turn out to be particularly useful when building distributed systems:

• Linearizable atomic operations
  • Using an atomic compare-and-set operation, you can implement a lock.
• Total ordering of operations
  • when some resource is protected by a lock or lease, you need a fencing token to prevent clients from conflicting with each other in the case of a process pause.
• Failure detection
• Change notifications

Summary

之前几章的 Summary 我都是随便看看，但这章的 Summary 真的有含金量，所以还是总结一波。

We looked in depth at linearizability, a popular consistency model: its goal is to make replicated data appear as though there were only a single copy, and to make all operations act on it atomically.

We also explored causality, which imposes an ordering on events in a system (what happened before what, based on cause and effect). Unlike linearizability, which puts all operations in a single, totally ordered timeline, causality provides us with a weaker consistency model: some things can be concurrent, so the version history is like a timeline with branching and merging. Causal consistency does not have the coordination overhead of linearizability and is much less sensitive to network problems.

However, even if we capture the causal ordering (for example using Lamport timestamps), we saw that some things cannot be implemented this way: We considered the example of ensuring that a username is unique and rejecting concurrent registrations for the same username.This problem led us toward consensus.

With some digging, it turns out that a wide range of problems are actually reducible to consensus and are equivalent to each other:

• Linearizable compare-and-set registers
  • The register needs to atomically decide whether to set its value, based on whether its current value equals the parameter given in the operation.
• Atomic transaction commit
  • A database must decide whether to commit or abort a distributed transaction.
• Total order broadcast
  • The messaging system must decide on the order in which to deliver messages.
• Locks and leases
  • When several clients are racing to grab a lock or lease, the lock decides which one successfully acquired it.
• Membership/coordination service
  • Given a failure detector (e.g., timeouts), the system must decide which nodes are alive, and which should be considered dead because their sessions timed out.
• Uniqueness constraint
  • When several transactions concurrently try to create conflicting records with the same key, the constraint must decide which one to allow and which should fail with a constraint violation.

All of these are straightforward if you only have a single node, or if you are willing to assign the decision-making capability to a single node. This is what happens in a single-leader database: all the power to make decisions is vested in the leader, which is why such databases are able to provide linearizable operations, uniqueness constraints, a totally ordered replication log, and more.

However, if that single leader fails, there are three ways of handling that situation:

• Wait for the leader to recover, and accept that the system will be blocked in the meantime.
• Manually fail over by getting humans to choose a new leader node and reconfigure the system to use it.
• Use an algorithm to automatically choose a new leader. This approach requires a consensus algorithm, and it is advisable to use a proven algorithm that correctly handles adverse network conditions.

Although a single-leader database can provide linearizability without executing a consensus algorithm on every write, it still requires consensus to maintain its leadership and for leadership changes.