Extensive Reading

Author Info

Background

  • State-of-the-art on-device inference frameworks fall back to the CPU/GPU for the attention operation , which is necessary for accuracy but causes resource contention and degrades user experience.
  • Running the full attention operation directly on the NPU is not a viable alternative, as its high sensitivity to quantization results in significant accuracy degradation (an 18 pp average drop) when using the NPU’s low-precision integer compute.
  • Applying traditional sparse attention on the CPU/GPU to lessen the workload yields minimal performance gain, as the required estimation stage to find important tokens becomes the new computational bottleneck.

Insights

Compute sparse attention accurately and efficiently in NPU-centric LLM inference

利用 LLM 的稀疏注意力的调整，每次推理时在 NPU 上量化后的低精度 Q,K 计算注意力分数排名，得到前 20% 的 index, 在 CPU 上实现稀疏注意力计算

Challenges

  • The inflexibility of NPU static compute graph
    • Solution: NPU compute graph bucketing
  • Mulit-faceted NP-hard NPU-CPU/GPU scheduling
    • Solution: Head-wise NPU/CPU/GPU pipeline

Approaches

NPU Features

  • Integer accelerator for DNN inference
    • Zero or relatively low float capabilities

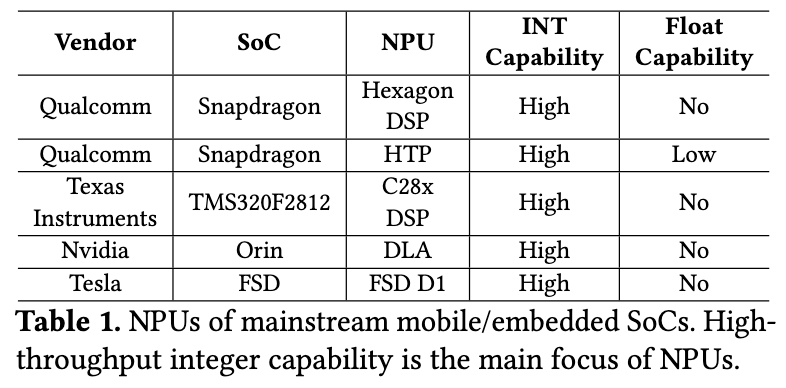
pasted-image-20251113105947

  • Static compute graph
    • Scale factors and tensor shapes are fixed in a graph

pasted-image-20251113110025

Sparse Attention

Workflow of sparse attention:

  • Estimate:
    • $attn\_score=softmax(mask(\dfrac{QK}{\sqrt{d_k}}))$
    • Top k values are selected with their indices transferred to the next stage
  • Attention
    • Only the tokens that are retained by the indices are involved
    • $O=softmax(mask(\dfrac{QK}{\sqrt{d_k}})) \cdot V$

pasted-image-20251113110856

The estimation stage requires processing all tokens, dominating the overall computation

One key observation is only determining the important positions in Q·K is less prone to quantization compared to calculating the exact value of the QKV result.

The rationale is that determining the important tokens only requires the relative value

So we can estimate the score in INT8 on NPU!

shadowAttn

This paper observes that the importance of heads and layers is uneven, so the ratios between different heads should be tailored according to the importance

The rationale behind the unevenness is mainly that various parts of a neuron network may learn various aspects of the data

pasted-image-20251113111409

The importance score can be calculated by the following formulas:

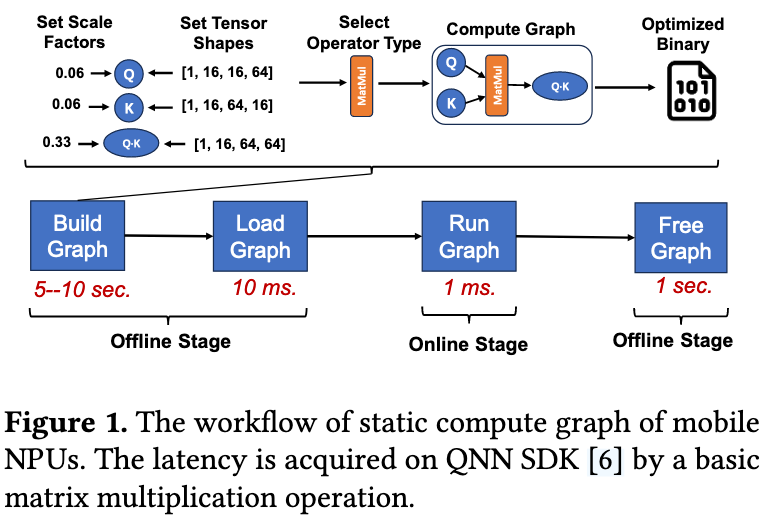
$$headImp_i=loss(head_i=0,C)-loss(C)$$$$layerImp_i=loss(layer_i=0,C)-loss(C)$$

Overall workflow

  • The offline stage
    • shadowAttn determines a sparse ratio for each separated head based on its importance and global sparsity ratio
    • generate and organize multiple static graphs
  • The NPU-centric compute graph
    • Generate a sparse attention module, the estimation of QK is running on NPU in INT8
  • The online stage
    • Run the compute graph

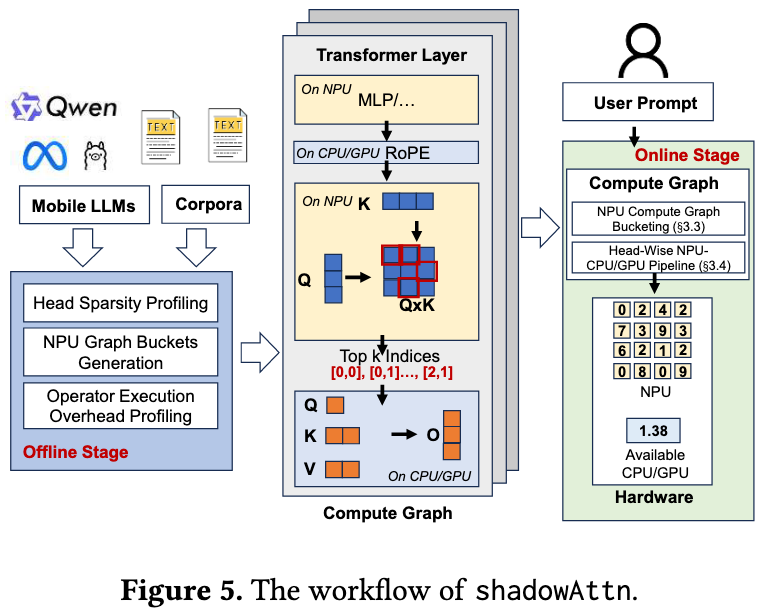
pasted-image-20251113111839

In the online stage, shadowAttn employs two specific optimizations to accelerate the process

  • NPU compute graph bucketing
    • Very intuitive, skip
  • Head-Wise NPU-CPU/GPU Pipeline
    • Organize under the granlity of head units

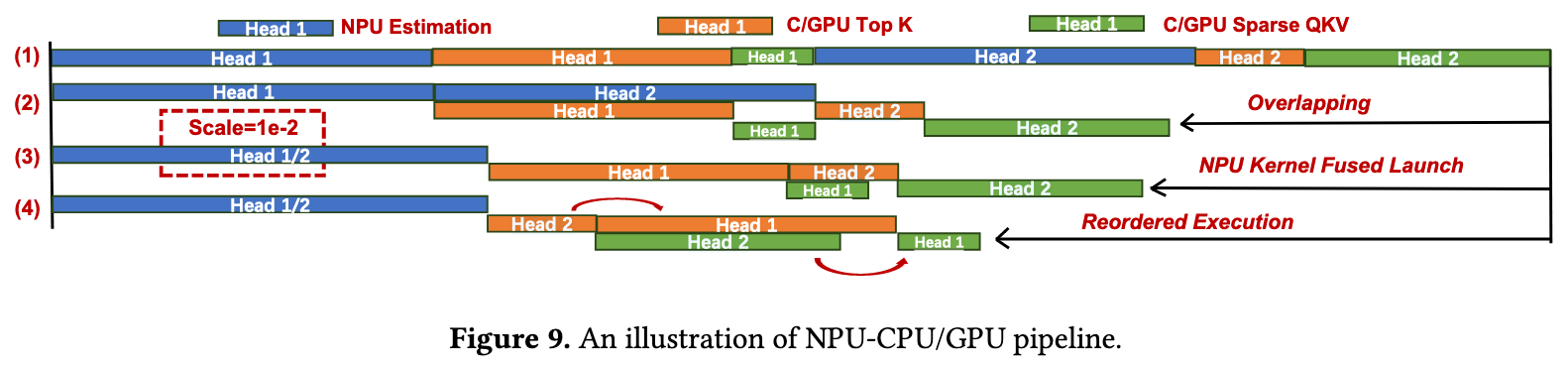
pasted-image-20251113112649

  • (2) -> (3): If head 1 and 2’s scale factor is the same, we can compute them together, which is faster since it avoids another NPU kernel launch
  • (3) -> (4): Reorder the execution on CPU to minimize the bubbles

Evaluation

Thoughts

When Reading

NPU compute graph bucketing 好像不是什么新技术，属于那种知道 NPU 特性限制后的人都能想出来？

Idea 很简单也很有效，一眼就能 work?

Xu Mengwei 这个团队是不是把端侧异构加速推理的 low-hanging fruits 全给摘完了？