Extensive Reading
Author Info
Background
- The Problem: Standard decoding applies the same computational power to every token generated. However, text generation has heterogeneous complexity. A complex logical deduction in a mathematical proof requires significantly more “intelligence” than generating routine connecting phrases (e.g., “therefore,” “it follows that”).
- The Limitation of Existing Solutions: Current optimization techniques, such as Speculative Decoding, are conservative. They prioritize perfect output fidelity, ensuring the output matches the large model exactly by verifying every token. The authors argue this is unnecessary for many applications.
Insights
- The paper’s Proposal: Entropy Adaptive Decoding (EAD).
- Dynamically switches between a small model ($M_S$) and a large model ($M_L$) during generation.
- Unlike speculative decoding, EAD accepts controlled output divergence—meaning the output might differ from what the large model would have produced alone, provided the reasoning remains sound.
So why not use EAD when divergence occurs in Speculative Decoding?
Approaches
The system uses entropy as a proxy for generation difficulty. High entropy in the probability distribution suggests uncertainty/complexity (requiring the Large Model), while low entropy suggests predictability (sufficient for the Small Model).
Entropy Calculation
For a given timestep $t$, the model produces logits $l$. The probability $p_i$ is calculated via softmax, and the entropy $H_t$ is derived before temperature scaling to capture true uncertainty:
$$H_t = -\sum_{i=1}^{V} p_i \log_2(p_i)$$Smoothing (Rolling Window)
To prevent the system from reacting to single-token fluctuations, the authors use a rolling window of size $w$ (experimentally set to $w=5$) to calculate the average entropy $\overline{H}_t$:
$$\overline{H}_t = \frac{1}{w} \sum_{i=t-w+1}^{t} H_i$$Dynamic Switching Mechanism
The system switches models based on a threshold $\tau$ and a stability constraint $d_{min}$ (minimum duration, set to 10 tokens) to prevent rapid oscillation. The switching logic is defined as:
$$M_t = \begin{cases} M_L & \text{if } \overline{H}_t \ge \tau \text{ and } c \ge d_{min} \\ M_S & \text{if } \overline{H}_t \le \tau \text{ and } c \ge d_{min} \\ M_{t-1} & \text{otherwise} \end{cases}$$- High Uncertainty ($\overline{H}_t \ge \tau$): The system infers that the current text generation is complex (e.g., a reasoning step) and utilizes the Large Model ($M_L$).
- Low Uncertainty ($\overline{H}_t \le \tau$): The system infers that the generation is routine (e.g., scaffolding text) and utilizes the Small Model ($M_S$).
Does this will affect model’s accuracy? Since some critical tokens are likely averaged and result in being inferenced on the SLM instead of the LLM.
Evaluation
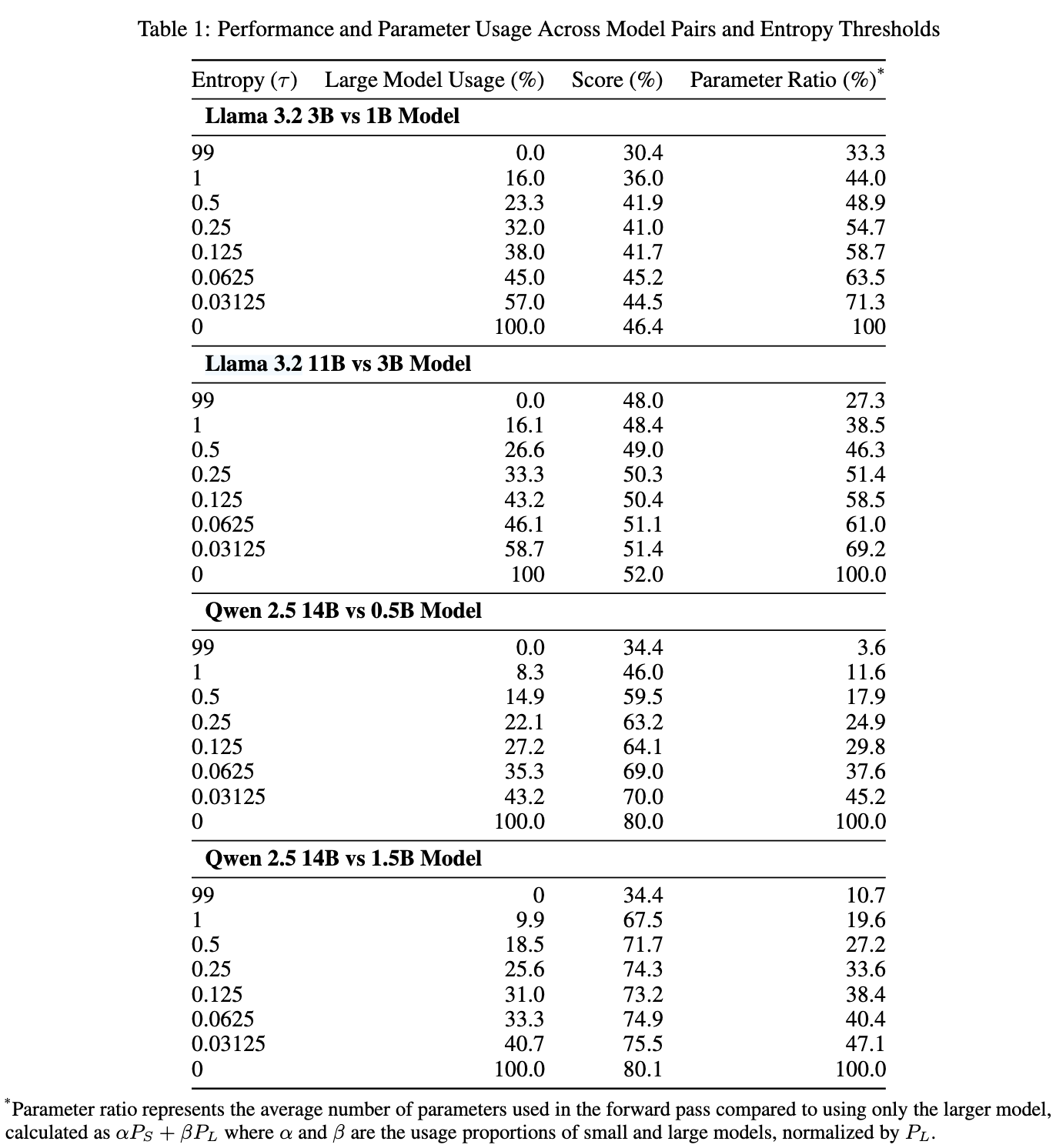
- LLM’s usage is too high, there is likely no wall time speed up at all.
- The comparison is not fare – The paper should involve Speculative Decoding
- The LLM’s usage is said to be 33.3%, that means LLM will run an inference step every 3 tokens on average, Speculative Decoding can do this too, and it is lossless
- This is no ablation study
- How does rolling window affect LLM’s usage and overall accuracy
- Hot does dynamic switching mechanism affect LLM’s usage and overall accuracy
- I am wondering the answers to these problems are not well
Thoughts
When Reading
Rolling window and dynamic switching mechanism can observably tackle the single-token fluctuation problem, but it will definitely degrade the accuracy, this paper didn’t detail it.
The LLM’s usage in experiments is too high to present practical values, why not use Speculative Decoding?
“Current optimization techniques, such as Speculative Decoding, are conservative. They prioritize perfect output fidelity”
So entropy based token level routing should outperform Speculative Decoding at least.