Estimating LLM Uncertainty with Evidence

Extensive Reading

Author Info

Background

Hallucinations exist in Large Language Models (LLMs) — where models generate unreliable responses due to a lack of knowledge.

Existing methods for estimating uncertainty to detect hallucinations are flawed:

• Failure of Probability-Based Methods: Traditional methods rely on softmax probabilities. The normalization process (softmax) causes a loss of “evidence strength” information.
  • A high probability does not always mean the model is knowledgeable; it might simply mean one token is slightly better than others in a low-knowledge scenario.
  • Conversely, a low probability might not mean ignorance; it could mean the model knows multiple valid answers (e.g., synonyms).
• Limitations of Sampling-Based Methods: Methods like Semantic Entropy require multiple sampling iterations, which is computationally expensive and fails to capture the model’s inherent epistemic uncertainty (e.g., consistently producing the same incorrect answer due to lack of training data).

Insights

The reason why probability-based methods fail to identify reliability is that probability is normalized.

The authors propose LogTokU, a framework that uses raw logits (before normalization) as evidence to decouple uncertainty into two distinct types.

Decoupling Uncertainty

Instead of a single scalar probability, LogTokU separates uncertainty into:

• Aleatoric Uncertainty (AU): Data uncertainty. It reflects the relative confusion between tokens (e.g., “is the next word ‘happy’ or ‘glad’?”).
• Epistemic Uncertainty (EU): Model uncertainty. It reflects the absolute strength of evidence the model has for its prediction, derived from the magnitude of the logits.

The Four-Quadrant Framework

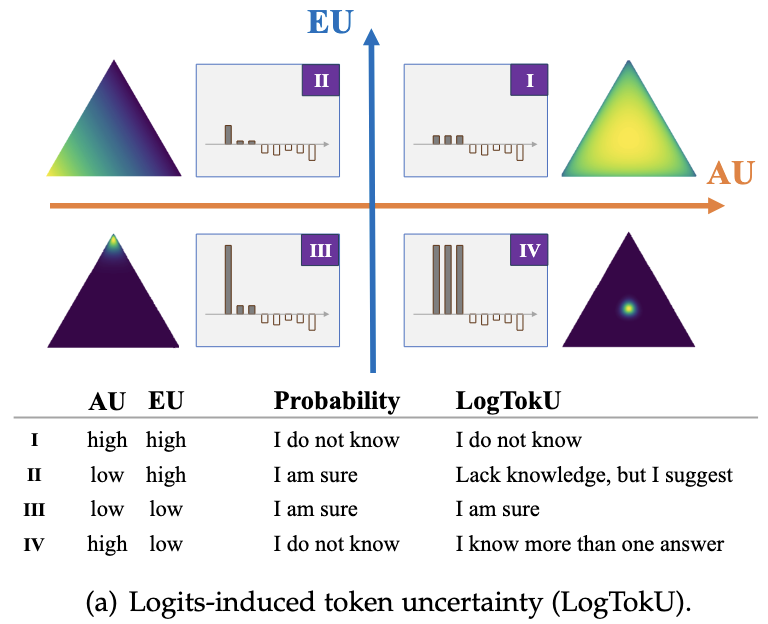
By combining AU and EU, the paper defines four distinct cognitive states for the LLM, which probability-based methods often conflate:

• Quadrant I (High AU, High EU): “I do not know.”
  • The model has low evidence for all options and is confused. This indicates a lack of knowledge and an unreliable response.
• Quadrant II (Low AU, High EU): “Lack knowledge, but I suggest.”
  • The model generally lacks evidence (high EU) but has one token slightly stronger than others (low AU).
  • Failure of probability-based methods: Probability-based methods may regard this quadrant as highly reliable. However, it still involves a certain degree of risk due to the lack of knowledge, and the high probability only indicates the model recommendation.
• Quadrant III (Low AU, Low EU): “I am sure.”
  • The model has strong evidence for a specific token and low confusion. This is a reliable state.
• Quadrant IV (High AU, Low EU): “I know more than one answer.”
  • The model has strong evidence for multiple tokens.
  • Failure of probability-based methods: Probability methods often mistake this for uncertainty (low probability per token), but it is actually a reliable state where multiple valid options exist (e.g., punctuation or synonyms).

Approaches

Failures in Traditional Uncertainty Estimation

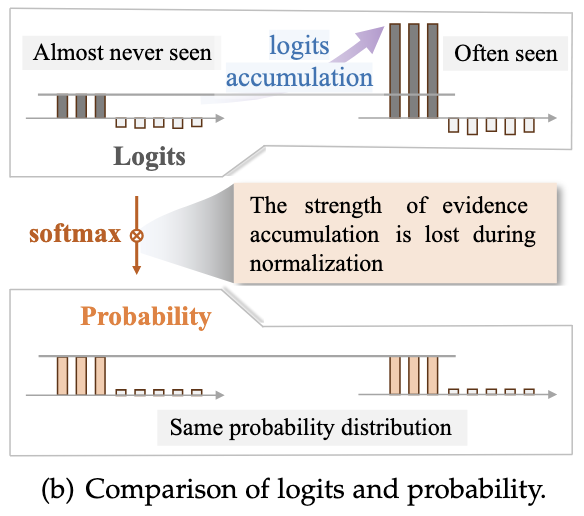
Probability is a normalization of the strength of evidence for different categories.

After logits are normalized into probabilities, the strength information of the evidence is lost:

LogTokU

To implement LogTokU, the authors adapt Evidential Deep Learning (EDL) principles to LLMs.

• Logits as Evidence: The method treats the top-$K$ logits as parameters ($\alpha$) of a Dirichlet distribution.
• Calculating Uncertainty:
  • Total Evidence ($\alpha_0$): The sum of the top-$K$ logits.
  • Epistemic Uncertainty (EU): Calculated as the inverse of the total evidence. Higher total logits (stronger evidence) result in lower EU.
  • Aleatoric Uncertainty (AU): Calculated as the expected entropy of the Dirichlet density.

This paper also gives two applications based on the LogTokU:

• Dynamic Decoding Strategy
  • Problem: A larger temperature tends to generate more unreliable responses from the model.
  • Solution: Higher temperature in low EU, lower temperature in high EU.
• Response Uncertainty Estimation
  • Problem: A large number of uncritical tokens exhibit high uncertainty, making it difficult to map token uncertainty to sentence uncertainty.
  • Solution: The reliability of a sentence is determined by averaging the reliability of the tokens with the $K$-lowest reliability scores
  • Note: This is measure on a sentence, we might want it to be measured on a token.

Evaluation

Thoughts

When Reading

非常有意思，可以在 Token-level routing 的框架下实践一下

Semantic Entropy 可以调研一下，但是应该先把 Entropy-based Token Level Routing 看完

Related Works