Quest Query-Aware Sparsity for Efficient Long-Context LLM Inference

Extensive Reading

Author Info

• MIT HAN Lab

Background

In long-context inference:

• The KV cache grows linearly with context length ($L$).
• At each decoding step, the model must read the entire KV cache to compute attention.

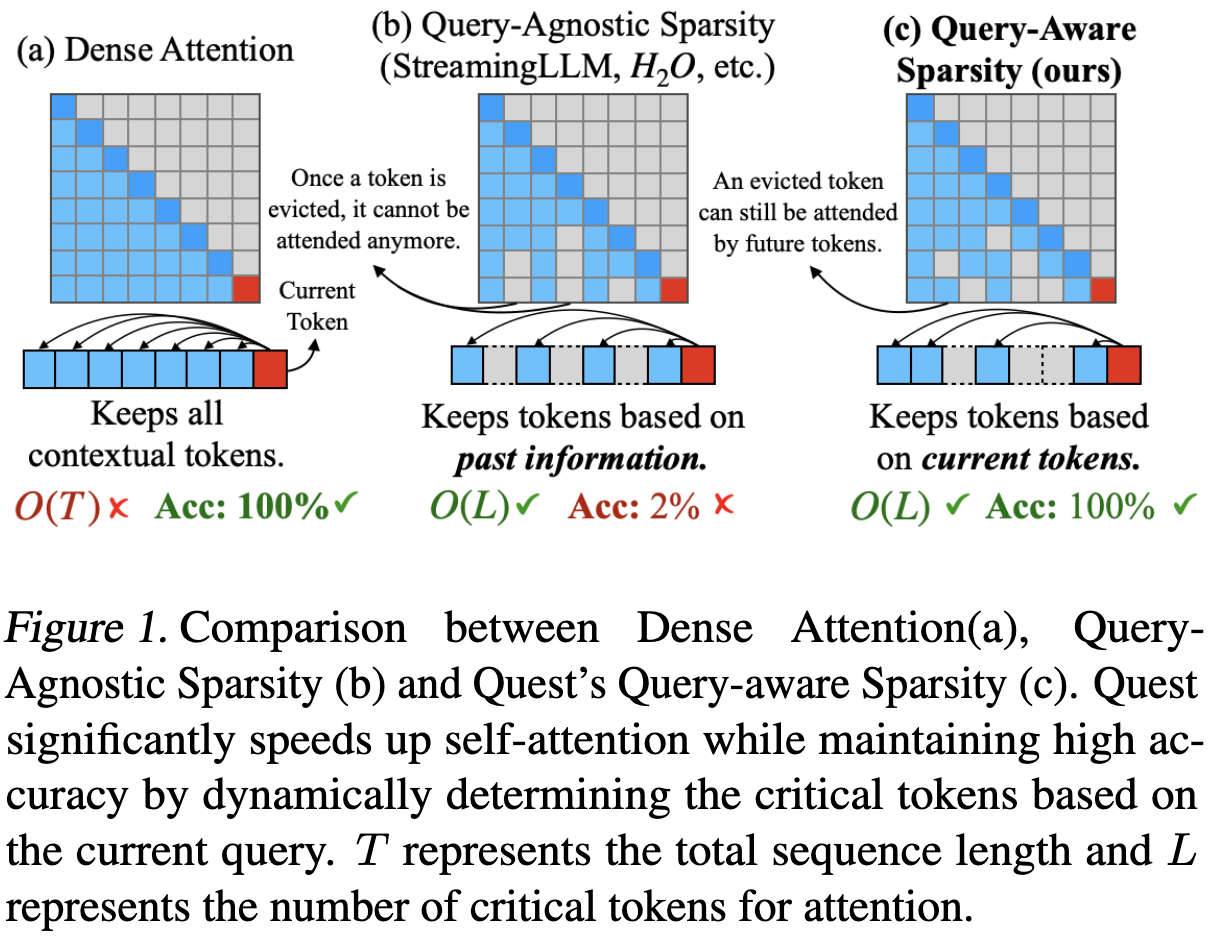
Existing works recognize there is small part of tokens that can domoinate the accuracy of token generation, and they choose to evict unimportant tokens:

• StreamingLLM keeps a sliding window plus a few “anchor” tokens.
• H2O, TOVA, etc., use heuristics or statistics to permanently drop “less important” tokens.

Once a token is evicted, it’s gone. BUT, the important tokens are Query-dependent.

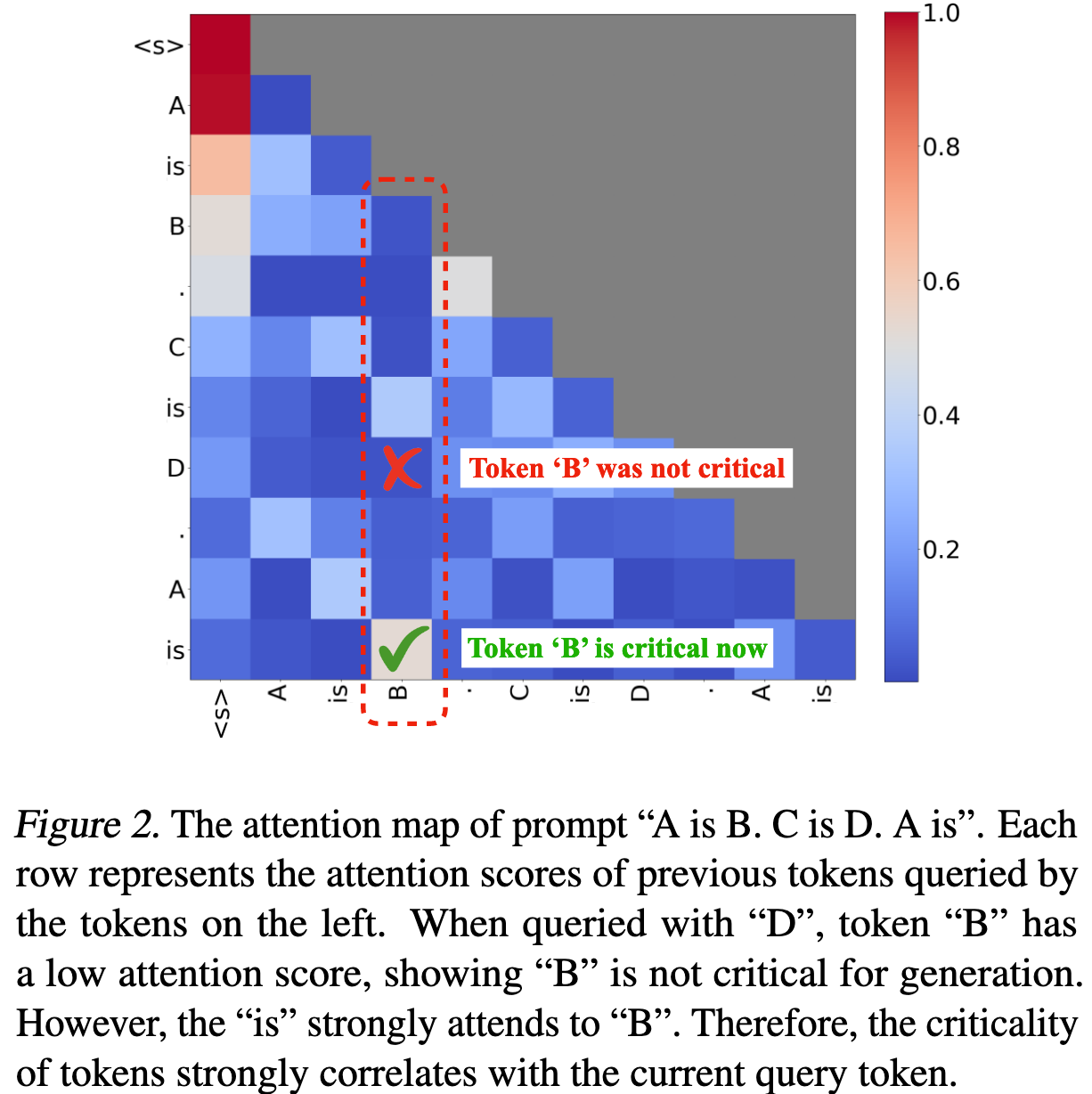
Given a sentence: “A is B. C is D. A is.” The token B’s importance varies (shown in Figure 2).

Insights

Don’t delete KV, just read the right part.

Approaches

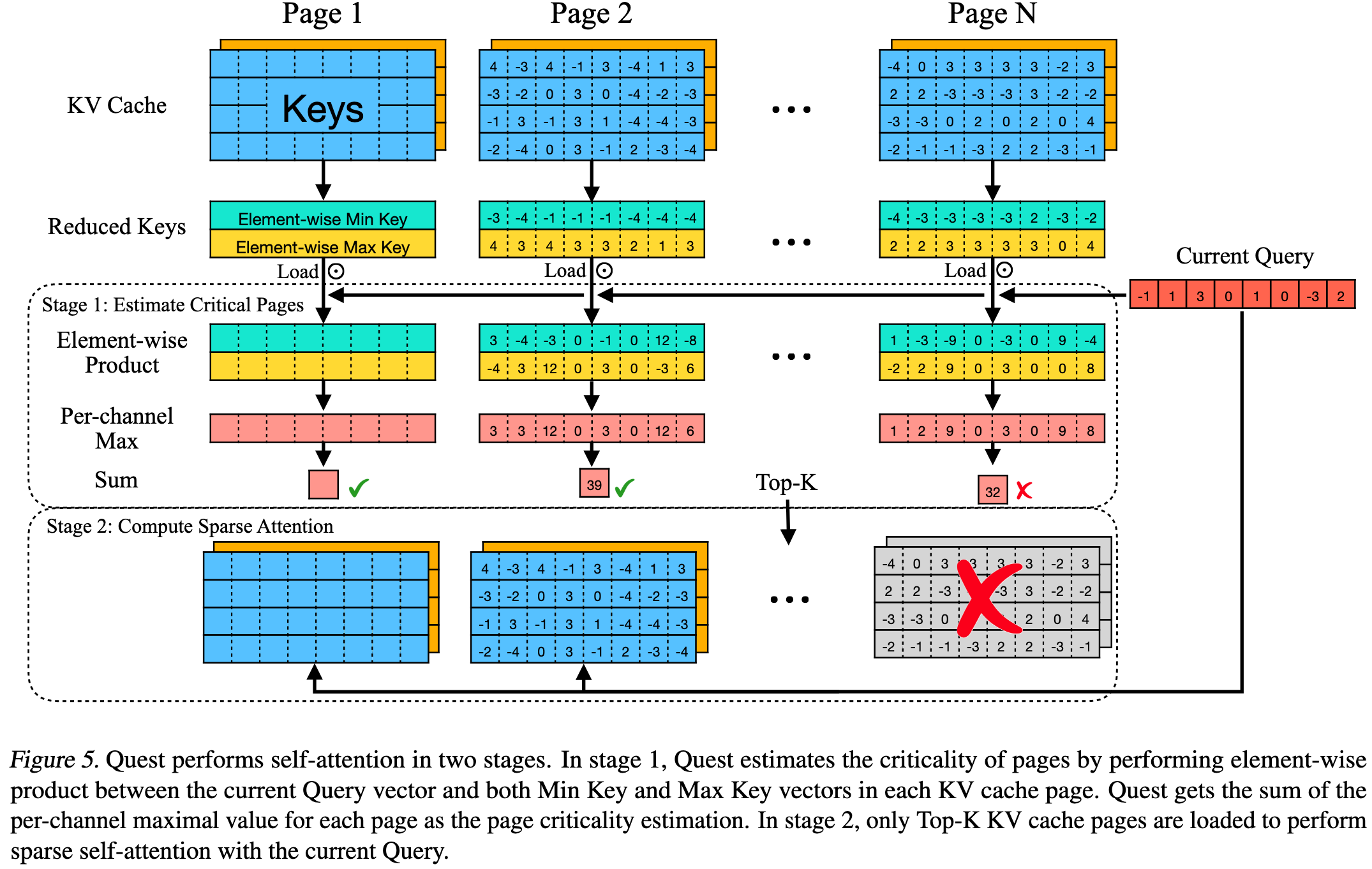
KV caches are organized in the form of pages (according to the PagedAttention).

Quest maintain some metadata per page: (two vectors)

• ($\mathbf{m}$): element-wise minimum over all keys in this page.
• ($\mathbf{M}$): element-wise maximum over all keys in this page.

Given the metadata ($\mathbf{m}, \mathbf{M}$), we know that for any key ($\mathbf{k}$) in the page, each dimension ($k_i$) must lie in ($[m_i, M_i]$). So for dimension (i):

• If ($q_i > 0$), the maximum product happens at ($k_i = M_i$).
• If ($q_i < 0$), the maximum product happens at ($k_i = m_i$).

So we can define:

$$ U_i = \max(q_i m_i,; q_i M_i) $$

Then the upper bound of the dot product between ($\mathbf{q}$) and any key in that page is:

$$ \text{score}(\text{page}) = \sum_i U_i $$

So we can run a Top-k selection over pages using these scores

Overall workflow:

• Query-aware page selection
• Sparse Attention on Selected Pages

Evaluation

Thoughts

When Reading

Talk is cheap, show me the code – CUDA everywhere

Related Works