SmoothQuant Accurate and Efficient Post-Training Quantization for Large Language Models

Extensive Reading

Author Info

• MIT HAN Lab

Background

• Modern large language models (LLMs) are extremely costly to serve in FP16 because of their massive parameter counts and long-context workloads; while low-bit quantization (especially INT8) is an attractive way to cut memory and latency, naïve post-training W8A8 (8-bit weights and activations) breaks down on large models due to severe activation outliers that cause large accuracy drops.

• Existing INT8 solutions either focus on weights only (e.g., GPTQ-style methods) or handle activation outliers with mixed precision (e.g., LLM.int8(), outlier-aware kernels); these approaches can preserve accuracy but often bring limited end-to-end gains because they leave activations/KV caches in higher precision, rely on complex custom kernels, or end up slower than plain FP16 in practical deployments.

• More advanced PTQ approaches (e.g., dynamic or group-wise quantization, outlier suppression via LayerNorm variants) alleviate some issues but still struggle to robustly quantize activations for very large LLMs under real hardware constraints, since they cannot easily use per-channel activation scaling inside standard GEMM kernels; this motivates a method that tames activation outliers while remaining fully compatible with simple, high-performance INT8 matrix multiplication.

Insights

Different tokens exhibit similar variations across their channels

We can say the values in activations follow power law distribution

Due to the characterics of INT8 GEMM kernels, when calculating $Y = X @ W$ we can only quantize:

• per-token (a row) in the $X$
• per-channel (a column) in the $W$

The most straightforward way (per-channel quantization) is not feasible, and it’s hard to quantize by using per-token due to the outliers in the token activation

We can “smooth” these outlier channels by scaling the weights accordingly to minimize the effect of outliers in the activations, leading to precisely per-token quantization

In a nutshell, $Y = X @ W$, outliers appear in the same columns of different tokens(same column in the activation matrix), we can scale the corresponding channel in the weight matrix to make the rows in the activation matrix more uniform thus easier to quantize

Summary:

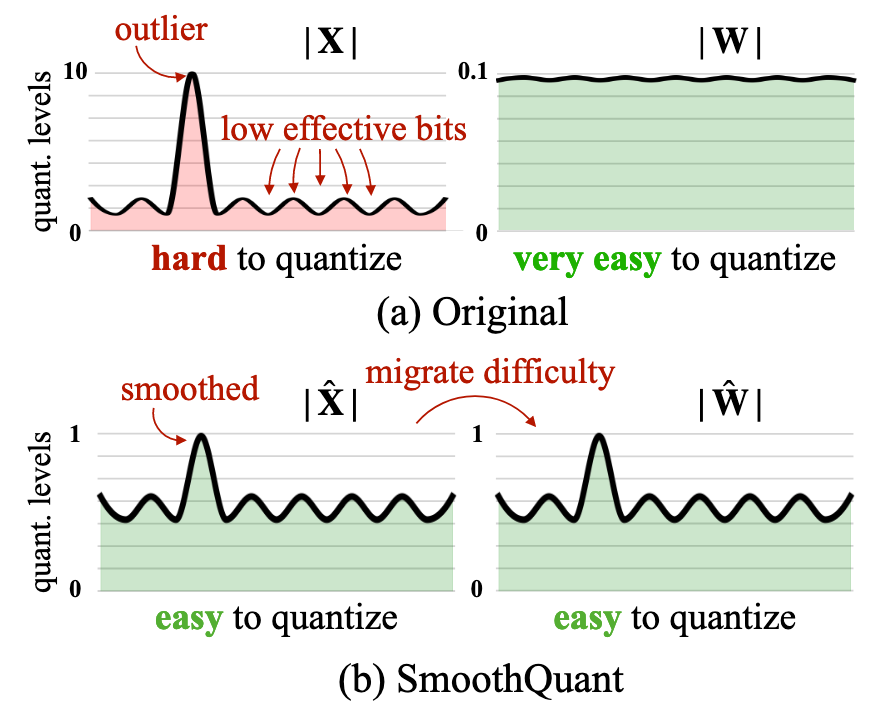
Origin:

• Activations are hard to quantize due to outliers
• Weights are very easy to quantization

SmoothQuant migrate diffculity from activations to weights by a mathmatical equivalent transformation:

• Activations are easy to quantize
• Weights are easy to quantize

Prequsitions

A channel is a column of the weight matrix – a dimention of the output features

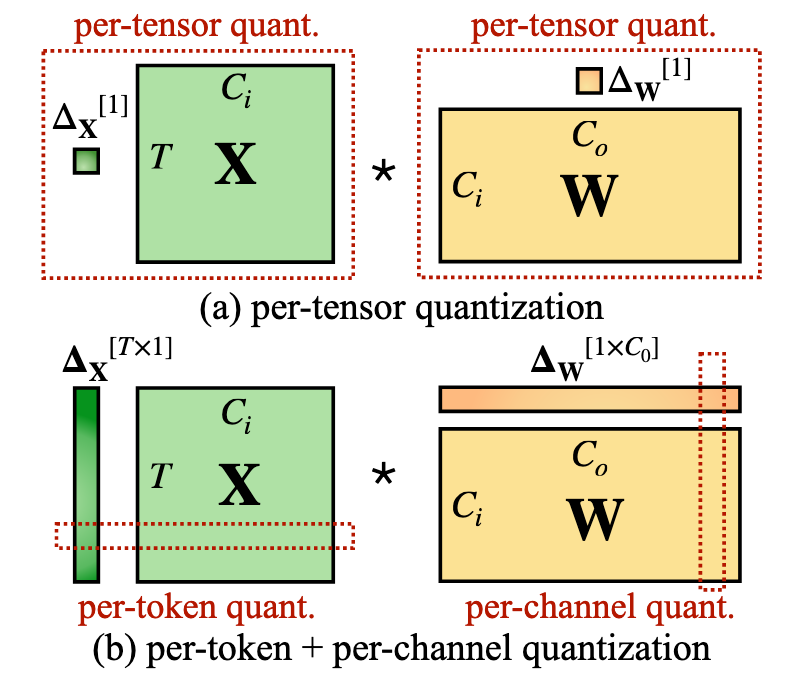
A basic matrix multiply is:

Loop form:

for m in 0..M-1:
  for n in 0..N-1:
    acc = 0
    for k in 0..K-1:
      acc += A[m,k] * B[k,n]
    C[m,n] = acc

For an LLM linear layer:

• (M = T) (tokens / batch*seq)
• (K = C_i) (input hidden dim, “in channels”)
• (N = C_o) (output hidden dim, “out channels”)

So:

• (A) ↔ activation (X \in \mathbb{R}^{T \times C_i})
• (B) ↔ weight (W \in \mathbb{R}^{C_i \times C_o})
• (C) ↔ output (Y \in \mathbb{R}^{T \times C_o})

Here, K = (C_i) is the inner dimension: it’s the one we sum over.

Simple symmetric quantization:

• Activations: $A_{\text{real}} \approx s_A(\cdot) \cdot A_{\text{int8}}$
• Weights: $B_{\text{real}} \approx s_B(\cdot) \cdot B_{\text{int8}}$

Suppose:

• (s_X) depends on N (per-row / per-token) or is global per-tensor
• (s_W) depends on C_o (per-col / per-output-channel) or is global

So:

• (s_A(m)): scale for row (m) of A (per-token)
• (s_B(n)): scale for column (n) of B (per-output-channel)

Then:

Note:

• (s_A(m)) and (s_B(n)) do not depend on (k),
• So we can pull them out of the summation:
  • Inner loop (over $k$) is pure INT8×INT8→INT32
  • We can only multiply by (s_A(m)s_B(n)) once per output element

So the whole process could be:

1. Run the integer GEMM (General Matrix-Matrix Multiplication)

C_int32 = A_int8 @ B_int8

2. for each element

for m in 0..M-1:
  row_scale = s_A[m]
  for n in 0..N-1:
    col_scale = s_B[n]
    C_real[m,n] = (row_scale * col_scale) * C_int32[m,n] + bias[n]

The Equation 2 is the same meaning (but there are no extra two diga matrix multiplications):

About W8A8 quantization:

• Weights are always quantized into INT8
• Activations keep in FP16 most of the time, because the activations will go into GELU/LayerNorm/etc

So we can quantize activations just-in-time for the GEMM (linear)

activation flow is FP16, only quantize to INT8 before GEMM

Activations are input-dependent, so there are two strategies to quantize:

• Dynamic quantization
  • For every GEMM, compute the scales based on its current states
• Static quantization
  • Use calibration data to estimate the typical range of activations for each layer
  • Fix a scale per layer offline

Approaches

How to smooth the activations?

To keep the mathmatical equivalence:

To balance the diffculity of quantization in activations and weights, SmoothQuant introduces a hyper-parameter:

We can regard quantization $Q(x)$ is not a linear operation, so transformation can work

Evaluation

Thoughts

When Reading

Understanding the mechinism of this paper can give you a comprehensive understanding of how quantization does underneath the inference process

Related Works