Extensive Reading
Author Info
Background
Long-Context Transformer Models (LCTMs) are increasingly needed (e.g., long-document QA, long video understanding/generation), but prefill attention is a major bottleneck because standard attention scales quadratically with sequence length.
Insights
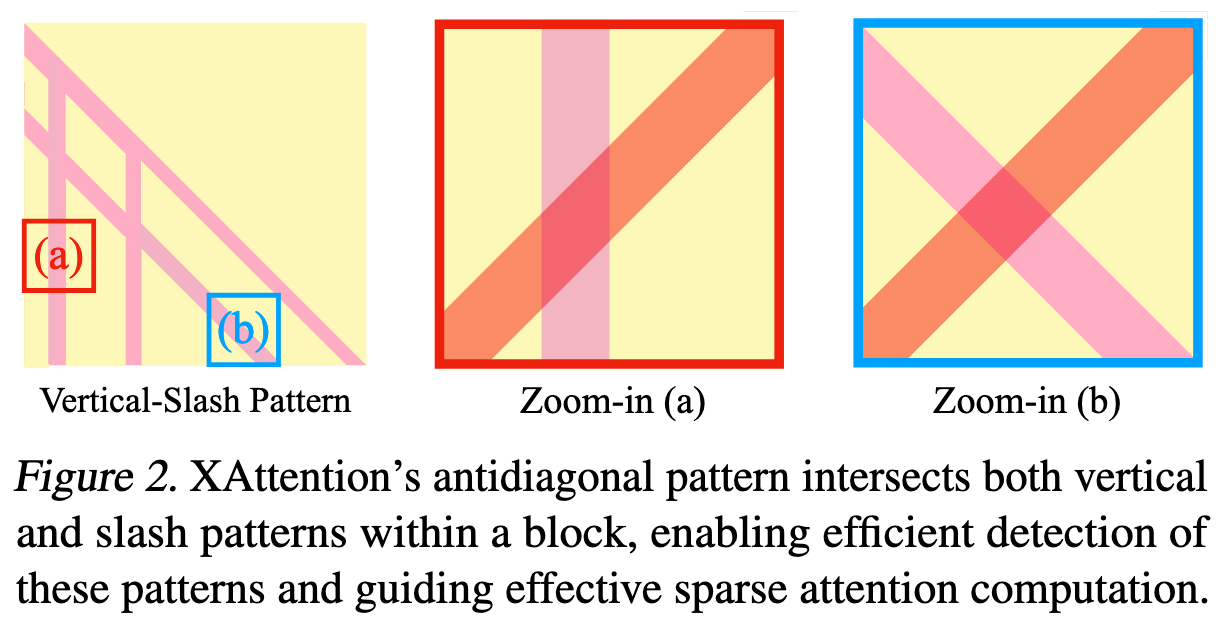
在一个 Block 中用反对角线可以捕捉到 Vertical-Slash Pattern 的中每个部分,假设整个 Pattern 很稀疏,那么只要包含了 Vertical/Slash 的 BLock 的得分就会很大,因此更容易被选出来
为什么反对角线有帮助:
- 信息覆盖:通过提出的跨步反对角线选择,每个标记都至少对一个反对角线和做出贡献(因此不太可能错过重要区域)。
- 模式检测:反对角线与块内常见的垂直和斜线稀疏模式相交,因此它们可以在不明确搜索这些模式的情况下检测到它们。
可以认为这篇文章的前提就是每个头都遵循 Vertical-Slash Pattern?
Challenges
整体看下来,理念很简单,但是具体的怎么算的 (Algorithm1) 还挺难理解的,必须手动模拟一遍,建议大小为 B=4, S=2

其中最重要的一步是基于步长的降维采样
假设:L=16, d=4, B=4, S=2
所以 Q: (16, 4), K: (16, 4)
我们先看一下循环范围:
- 外层循环 Q, 每次处理 Q 的一个 Block 大小,也就是 (4, 4)
- 内层需要处理所有 K,也就是 (16, 4), 可以看作需要处理 4 个 K Block
然后通过步长来提取分组
Q_reshape 的形状为 (2, 2, 4),可以理解为是这么布局的:矩阵的批次为2, 也就是有两个矩阵
第一个矩阵为 $\begin{bmatrix} \text{Row}_1 \\ \text{Row}_3 \end{bmatrix}$, 第二个矩阵为 $\begin{bmatrix} \text{Row}_0 \\ \text{Row}_2 \end{bmatrix}$
我们这里只关心一个 K Block 的情况,多个 K Block 的情况同理
K_reshape 的形状为 (2, 2, 4)
第一个矩阵为 $[Col_0, Col_2]$, 第二个矩阵为 $[Col_1, Col_3]$
按照 BMM 的运算,进行矩阵乘法后两个批次计算出的注意力分别对应原 Block 中的以下几个点:
- (1, 0), (1, 2), (3, 0), (3, 2)
- (0, 1), (0, 3), (2, 1), (2, 3)
这 8 个点正好是一个 4 x 4 Attention Block 中对角线上的点
这样计算量由原来的 $B^2D$ 降低为了 $\dfrac{1}{S}B^2D$
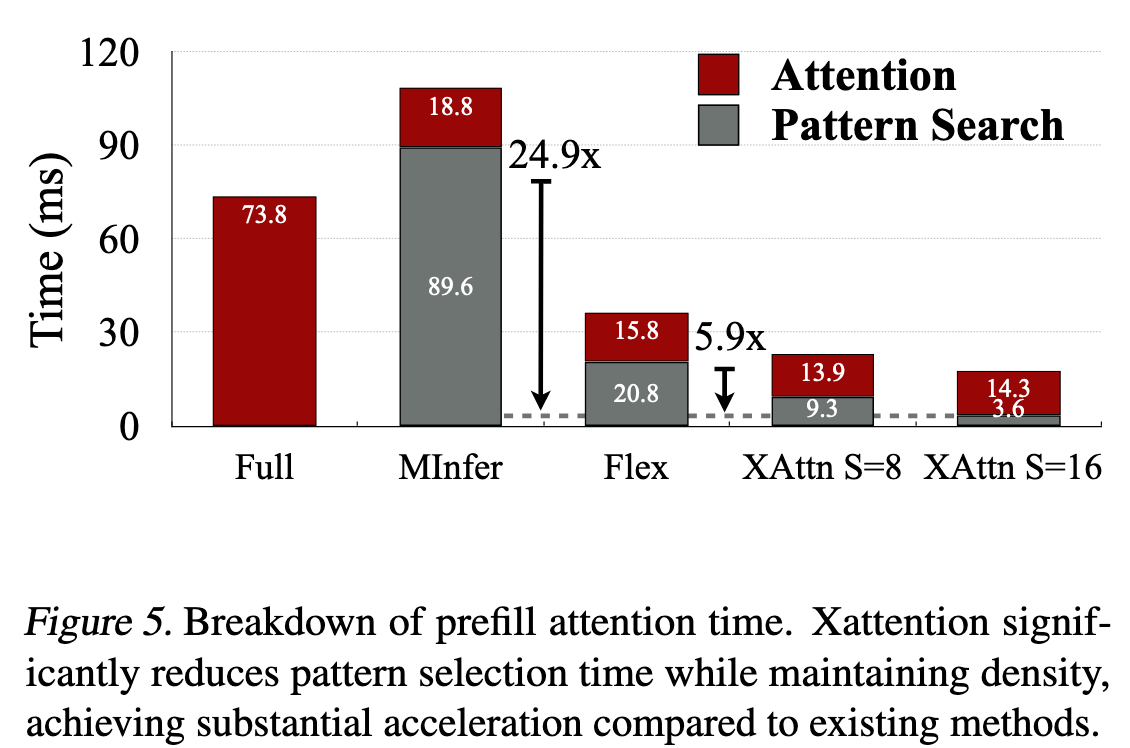
从 Evaluation 部分的 Figure 5 可以看出,数据完全对的上
- Full Attention 需要 73.8ms
- S=8 时 Pattern Search 需要 9.3ms,是 Full Attention 的八分之一
- S=16 时 Pattern Search 需要 3.6ms,大概也是 Full Attention 的十六分之一
Approaches
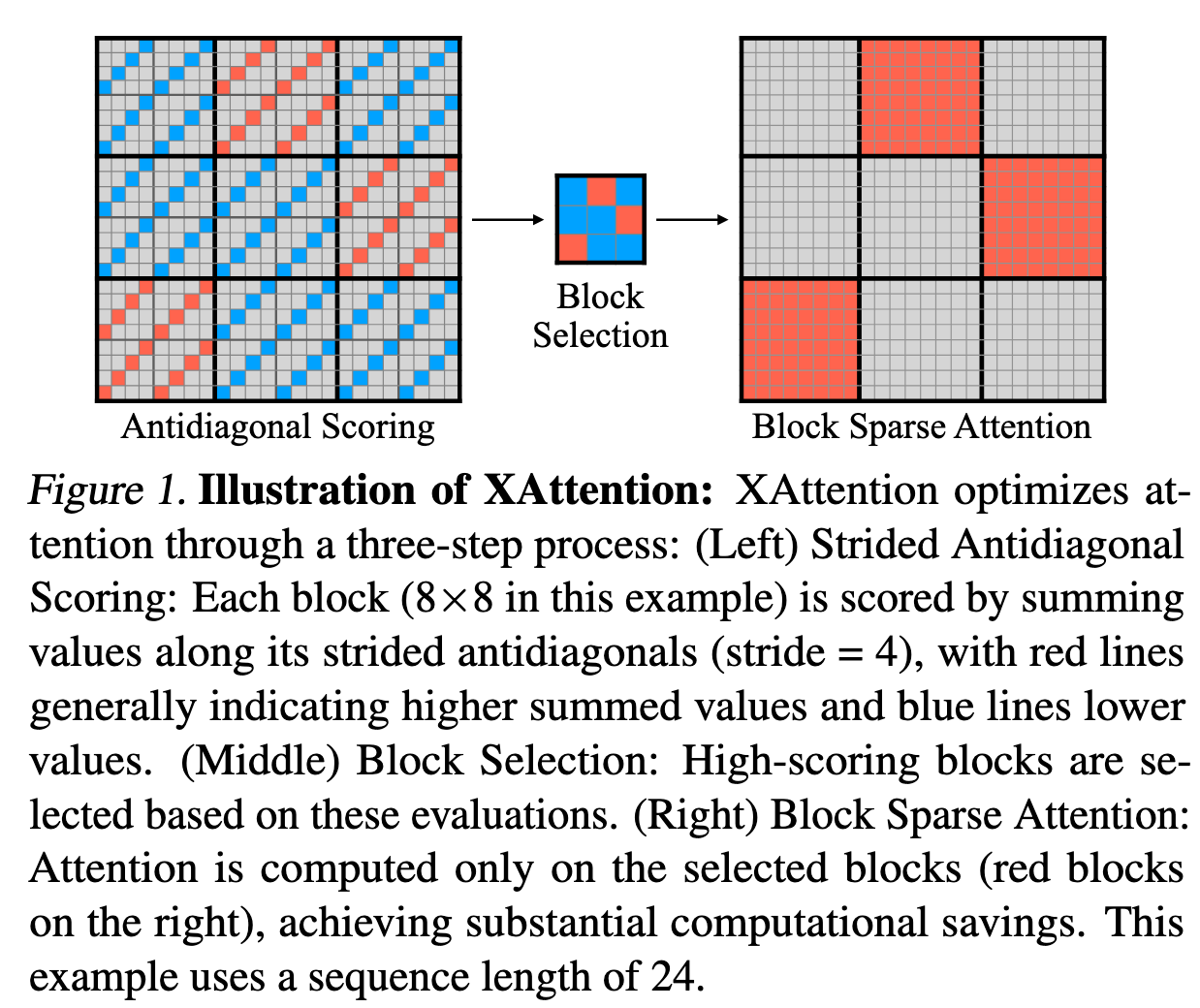
如何判断某个 Block 是否重要?
- 使用反对角线打分
如何选择 Block?
- 通过阈值累积质量目标进行块选择, 和 FlexPrefill A Context-Aware Sparse Attention Mechanism for Efficient Long-Sequence Inference类似
XAttention 还为每个 Attention Head 设置了一个动态的阈值,采用了动态规划算法
这算法部分我没太看懂,不管了,从消融实验上看不是很重要
Evaluation
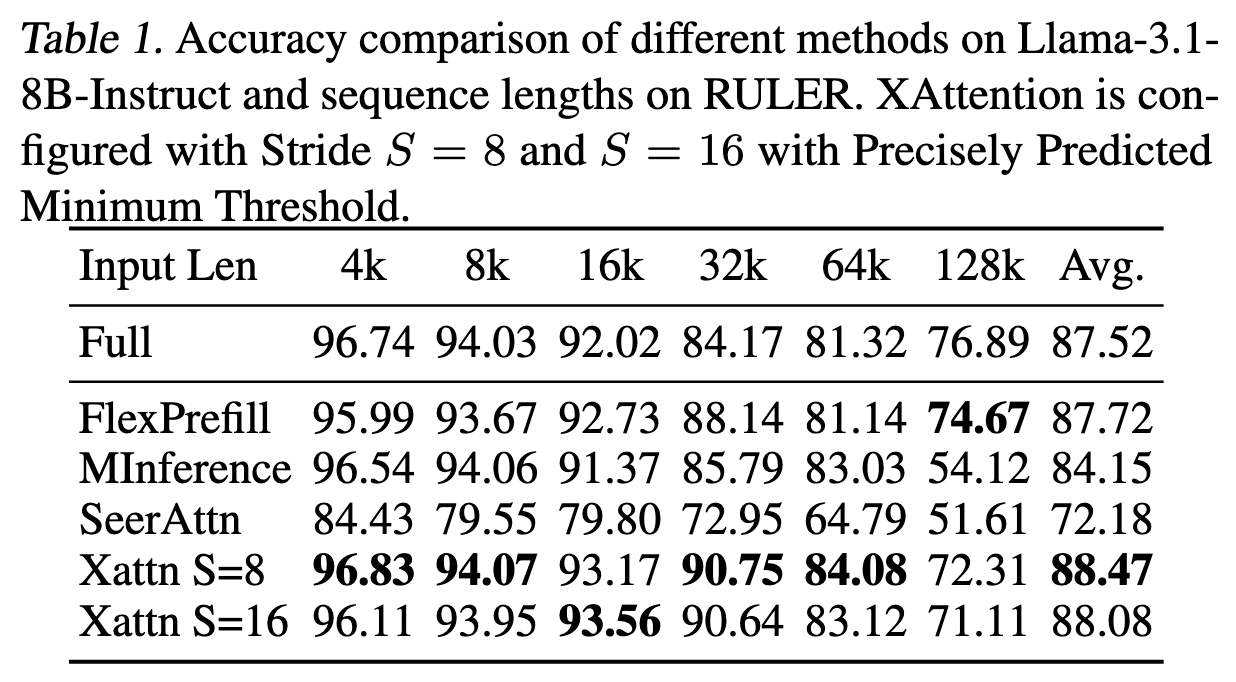
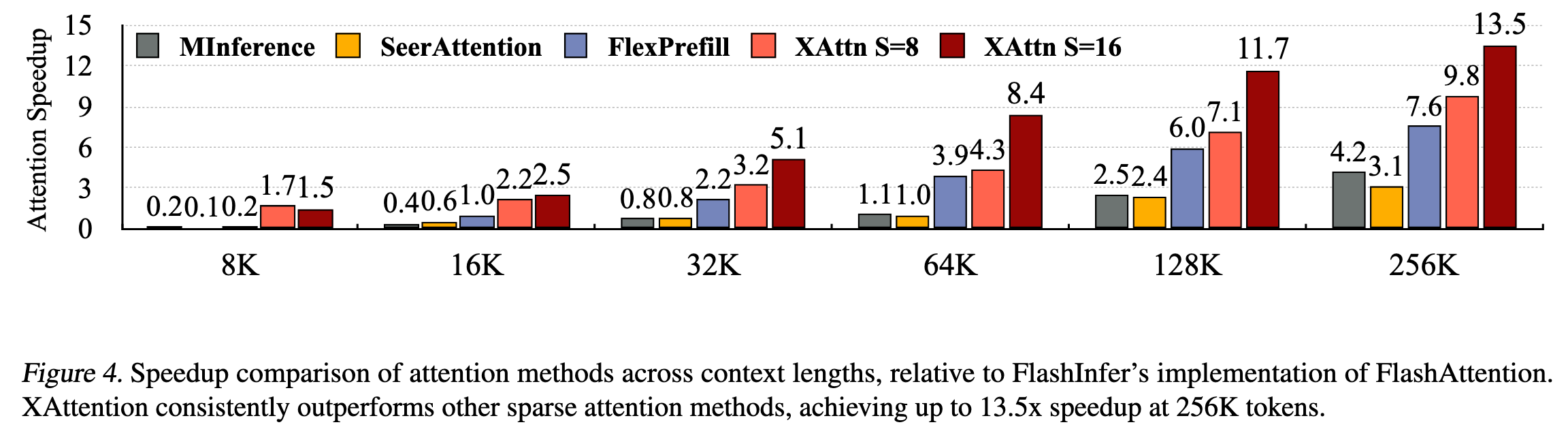
Thoughts
Openview
XAttention: Block Sparse Attention with Antidiagonal Scoring | OpenReview
- 我和大部分 Reviewer 都有相似的困惑,为什么反对角线的模式能够 work,但感觉作者还是在重复论文中的那两点
- 其中有一个 Reviewer 提出 ”用反对角线模式计算出的重要块与用原始注意力分数或池化注意力分数计算出的重要块在统计上是否一致?“ 的问题,作者采用了多种统计学证明确实有效,我觉得这个实验结果应该被放到附录中 – 非常有意思的是,这篇文章没有任何附录
- 有两个作者提到了其贡献属于 incremental
When Reading
Block Sparse Attention 都可以分为这么两步:
- 如何判断某个 Block 是否重要
- 如何选择重要的 Block 集合
不愧是 Han Lab 的作品,已经大道至简了,原理看起来很简单,但是算法实现本身还挺有意思的