Happened Before 关系
论文先从事件之间的 Happened Before 关系开始讲起

结合上图我们举例解释一下「Happened Before」关系:
- 同一进程内部先后发生的两个事件之间,具有「Happened Before」关系。比如,在进程 Q 内部,q_2 表示一个消息接收事件,q_4表示另一个消息的发送事件,q_2 排在 q_4 前面执行,所以 q_2 → q_4。
- 同一个消息的发送事件和接收事件,具有「Happened Before」关系。比如,p_1 和 q_2分别表示同一个消息的发送事件和接收事件,所以 p_1→ q_2;同理, q_4→ r_3。
- 「Happened Before」满足传递关系。比如,由 p_1→ q_2, q_2→_q_4和 q_4→ r_3,可以推出 p_1 → r_3。
作者然后说明了并发的概念:
Two distinct events a and b are said to be concurrent if a !→ b and b !→ a.
同时作者也描述了与因果性的关系:
Another way of viewing the definition is to say that a→b means that it is possible for event a to causally affect event b. Two events are concurrent if neither can causally affect the other.
需要注意的是, Happened Before 关系是一种偏序关系。
逻辑时钟
Lamport 在定义事件之间的「Happened Before」关系时特意避开了物理时间。这也就意味着,对事件的「发生时间」进行度量,只能根据逻辑时钟。
为什么要定义逻辑时钟这个概念呢?我们前面讨论过,在分布式系统中我们经常需要对不同的事件进行排序。那么,为了实现这种排序操作,我们很自然地就需要对事件的发生进行一种数值上的度量。我们希望,可以通过比较事件的时间戳数值大小,来判断事件发生的次序(即「Happened Before」关系)。这就好比我们通过看钟表上显示的数值来确定时间的流逝一样。
当然,逻辑时钟在给事件打时间戳的时候,必须要满足一定条件的。这个过程必须能在一定程度上反映出事件之间的「Happened Before」关系。
论文定义了一个时钟条件 (Clock Condition):
- 对于任意的事件 a 和 b:如果 a→b,那么必须满足 C〈a〉 < C〈b〉。
对于逻辑时钟的实现,论文也简单地给出了实现了两条规则:
- Each process $P_i$ increments $Ci$ between any two successive events.
- If event a is the sending of a message m by process $P_i$, then the message $m$ contains a timestamp $T_m= Ci (a)$.Upon receiving a message $m$, process $P_i$ sets $C_i$ greater than or equal to its present value and greater than $T_m$.
全局排序
引入逻辑时钟的目的是想帮助我们判断事件之间的 Happened Before 关系,但是由于该关系的偏序性,我们不能根据两个事件对应的时间戳在数值上的大小来推断出它们之间是否存在「Happened Before」关系。
In fact, the reason for implementing a correct system of logical clocks is to obtain such a total ordering.
对于不具有「Happened Before」关系的两个事件来说,它们对应的时间戳数值比较大小,是没有意义的。但是,确实可以根据两个时间戳的大小,来为两个事件「指定」一个次序。这个次序是人为指定的,并不是客观上要求的。
如果我们按照逻辑时钟给出的时间戳从小到大把所有事件都排成一个序列,那么就得到了分布式系统中所有事件的全局排序。
这里需要引入一个进程编号 $P_i$,如果两个进程的时间戳一样,那么人为指定进程编号小的事件先于进程编号大的事件发生,这样的话就可以定义一个全序关系 $\Rightarrow$ 。换句话说,它是把 “Happened Before” 关系补全为了一个全序关系。
在图中,就可以得到 $p_1$ => $r_1$ => $r_2$ => $q_1$ => $p_2$ => $q_2$ => $p_3$ => $q_3$ => $q_4$ => $q_5$ => $r_3$=> $p_4$ => $q_6$ => $r_4$ => $q_7$
在这个排序中,所有事件之间的「Happened Before」关系都被保持住了;而本来不存在「Happened Before」关系的事件之间,我们也依据时间戳的大小,通过人为指定的方式得到了一个次序。总之,我们得到了所有事件的一种全局排序,而这种排序是和「Happened Before」关系(即因果顺序)保持一致的。
有了全序关系后有什么用呢?论文用它解决了一个资源互斥问题:
多个 Process 共享一个集中资源 R,每个 Process 想使用 R 时必须申请,经过全部人同意后才可以使用,且使用完成后必须要释放 R 以供他人使用。且需要满足先申请先访问原则,还不能存在死锁的问题。
很容易想到的是使用协调者的解决方法:
- 存在一个至高无上的协调者管理资源分配;
- 协调者根据收到请求的先后顺序分配资源的使用顺序;
这个方案看起来一切正常,但是可能存在一个漏洞,假如:
- Process 1 向协调者发起资源分配请求 $R1$;
- Process 1 向 Process 2 发消息 M;
- M 触发 Process 2 产生事件,该事件也向协调者发起资源分配请求 R 2;
- R 2 先于 R1到达协调者
于是就不满足上面的先申请先访问的原则了。
暂时没想到该漏洞对应的实际例子,因为个人觉得如果两个获取锁的操作之间存在因果关系,那么第一个获取锁的操作成功后才应该向第二个进程发消息。
Lamport 提出的方案:
- 去掉协调者,改用分布式协调方案;
- 每个 Process 均有一个队列维护资源申请的消息,成为 RequestQueue
- P 申请资源时,向其他 Process 广播该资源申请消息,该消息是一个三元组<T, P, Action>;
- P 收到其他 Process 的资源申请消息时,将该消息放置于 RequestQueue 的尾部,并给申请者回复 ACK 消息;
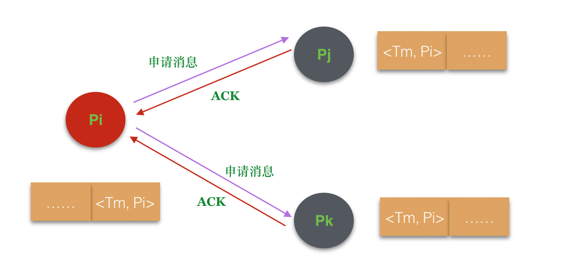
而 Pi 判断某个消息 (其实代表了一个事件,因为一般是事件申请资源访问,而消息只不过是代替事件去获得访问权限)能否获得资源的访问权限的条件:
- 该消息获得了所有节点的 ACK。
- 在本地的消息队列中没有比该消息更早的消息。
我们仔细品味下这两个条件:
- 获得所有节点的 ACK 这个比较容易理解,只有大家都同意了才可以访问;并且意味着这个事件已经被广播到了其他所有节点(有点像全序关系广播了)。
- 没有比该消息更早的消息则表示该消息是最早的申请者,注意,本地的消息队列中不仅有自己发出的资源申请访问的请求消息,还存有其他节点的资源申请访问请求;
- 如何判断两个消息先后顺序就采用了我们上面的全序定义方案,先判断 T,相同时再判断 P。
需要注意的是,本地的 Request Queue 中保存的请求消息可能会乱序,并非说队列头部是就是就旧的,队列尾部的就是最新的。因为多个节点之间存在消息传递上的延迟,先发出的请求有可能会后到达。因此,在判断时需要遍历队列上的所有消息。

论文中,这个算法后面的几段话也非常的有意思。
This approach can be generalized to implement any desired synchronization for such a distributed multiprocess system.
The synchronization is specified in terms of a State Machine.
Each process independently simulates the execution of the State Machine, using the commands issued by all the processes.
Synchronization is achieved because all processes order the commands according to their timestamps (using the relation $\Rightarrow$), so each process uses the same sequence of commands.
A process can execute a command timestamped T when it has learned of all commands issued by all other processes with timestamps less than or equal to T.
However, the resulting algorithm requires the active participation of all the processes. A process must know all the commands issued by other processes, so that the failure of a single process will make it impossible for any other process to execute State Machine commands, thereby halting the system.
只要我们获得了所有事件的全局排序,那么各种一致性模型对于读写操作所呈现的排序要求,很自然就能得到满足。 而更近一步,事件的全局排序结合状态机复制(State Machine Replication)的思想,几乎可以为任何分布式系统的设计提供思路。
逻辑时钟的异常行为
假设 Alice 和 Bob 是一对好朋友,他们住在两个不同的城市。Alice 在网络上观看足球比赛,现在她在自己的计算机上发出了一个查询请求(记为请求 A),用于查询比赛的比分。假设处理请求的是一个分布式系统,并且采用逻辑时钟来为请求打上时间戳。然后请求 A 返回了最新的比分。Alice 这时发现有了一个新的进球得分,于是她打电话给另一个城市的 Bob,告诉他去服务器上查询同一个比赛的比分结果。于是,Bob 通过自己的计算机发出了请求 B。由于系统采用了逻辑时钟,因此处理请求 B 的服务器有可能为请求 B 打上了一个比请求 A 更小的时间戳。对于逻辑时钟来说,这种行为属于正常情况。这是因为,一方面,逻辑时钟的定义特意避开了物理时间,系统产生的时间戳与请求的真实时间先后并没有直接关系;另一方面,在系统内部,请求 A 与请求 B 这两个事件之间,并不存在「Happened Before」关系,因此并不保证请求 B 的时间戳一定比请求 A 的时间戳更大。结果,请求 B 由于被打上了一个更小的时间戳,有可能在全局排序中排到了请求 A 的前面,所以 Bob 并没有查询到最新的球赛比分(也许只查询到了旧版本的数据,这里的行为取决于一些额外的数据库实现机制),因此与 Alice 看到的结果产生了不一致。
出现异常行为的原因在于系统不知道 Alice 给 Bob 打了电话,所以才认为给请求 B 打一个更小的时间戳是合理的。显然,让系统知道 Alice 给 Bob 打电话这个事实,是不太可能的。但我们注意到,如果考虑一下请求 A 和 B 发出的时间先后,这个问题可能就有办法解决了。
在这个例子中,Alice 给 Bob 打电话起码要花上几分钟,也就是说请求 B 发生的时间比请求 A 要晚几分钟。对于晚了这么久的请求 B,系统仍然给打了一个更小的时间戳,根本原因在于逻辑时钟是没有和真实的物理时间绑定的。因此,我们可以得到结论:仅仅使用逻辑时钟是不够的,需要使用物理时钟才行。又因为我们需要一个分布式的系统,所以物理时钟不能只有一个实例,而是最好每个进程都有自己对应的本地物理时钟。否则,运行物理时钟的进程就会成为单点,也就失去了分布式的意义。
现在我们假设,如果系统的物理时钟满足这样一个最苛刻的条件:即使 Alice 通知 Bob 的速度达到光速,系统也总是能保证对请求 B 打上的时间戳要大于请求 A 的时间戳,那么,就能保证永远不出现前面的异常行为。这样的一个时钟条件,在 Lamport 的论文中被称为 Strong Clock Condition。具体描述如下:
- 对于任意的事件 a 和 b:如果 a➜b,那么必须满足 C〈a〉 < C〈b〉。
- “→”表示「Happened Before」关系
- “➜”表示由相对论定义的事件偏序关系
时空本身定义了一种偏序
这里涉及到了光锥的概念:
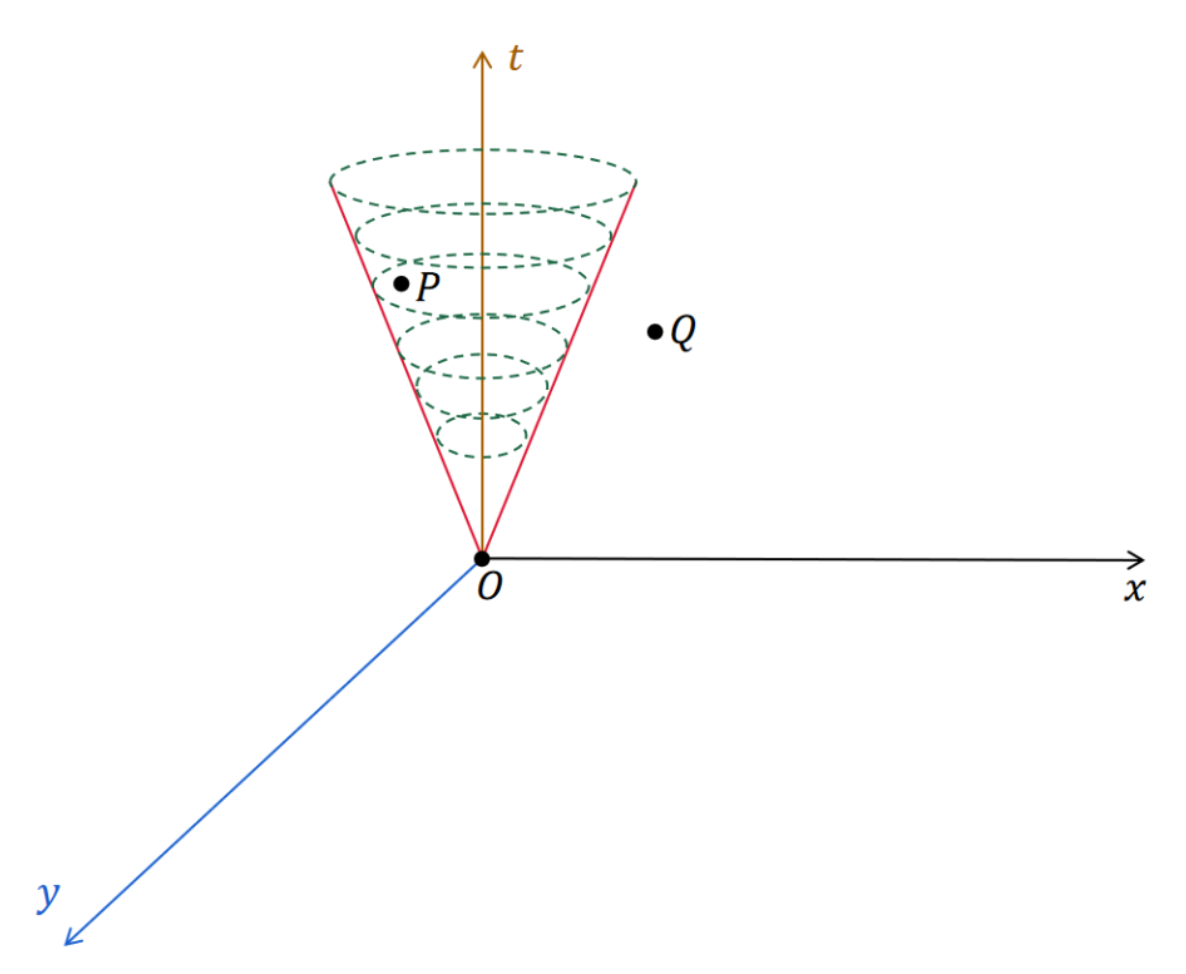
根据相对论,任何信息传递的速度,最快就是光速。而一个事件要想对另一个事件产生影响,至少要在那个事件发生之前传递一定的信息到达所在的空间位置。因此,一个事件所能够影响的范围,就是以它为顶点的未来光锥内部的时空区域。以上图为例,点 P 在点 O 的未来光锥内部,因此事件 P 可能受到事件 O 的影响;而点 Q 在点 O 的未来光锥外部,因此事件 Q 不可能受到事件 O 的影响。
这些事件之间可能产生的影响关系,就是我们上一章节末尾所提到的事件偏序关系“➜”。例如,对于事件 O 和事件 P 的关系,我们可以用符号表示成:O➜P。但事件 O 和事件 Q 之间就不存在 O➜Q 的关系。
简单总结一下,就是:
- 一个事件可能对它的未来光锥内部的任何事件产生因果性上的影响。
- 一个事件与它的未来光锥内部的任何事件之间,满足一个偏序关系,即“➜”。
物理时钟同步算法
对于任意两个有偏序关系的事件(或者说可能在因果性上产生影响的两个事件),我们的物理时钟要保证总是会为后一个事件打上一个更大的时间戳。
要实现这个目标,我们面临的障碍主要来源于物理时钟的两种误差:
- 时钟的运行速率跟真实时间的流逝速率可能有差异;
- 任意两个时钟的运行速率有差异,它们的读数会漂移得越来越远。
Lamport 在论文中提出的物理时钟同步算法,做的事情其实就是,将这两种时钟误差考虑在内,不断地对各个进程本地的物理时钟进行微调,把误差控制在能够满足 Strong Clock Condition 的范围内。
- 对于进程内发生的不同事件,必须保证后发生的事件比先发生的事件时间戳要大。这实际上是要求我们保证每个物理时钟实例的读数总是单调递增的。
- 两种机制的赛跑:一方面,Alice 通过系统外的方式向 Bob 传递信息,只要这个过程足够快,他们就有可能“看到”时钟误差造成的时钟读数减退(也就是出现了异常行为);另一方面,物理时钟同步算法通过在时钟之间不断交换信息并按照一定规则调整时钟读数,将时钟误差控制在一定范围内。只要算法的各个参数设置得当,就能保证:即使 Alice 向 Bob 传递信息的速度达到物理极限——光速,他们也无法“看到”时钟读数的减退现象。于是,Strong Clock Condition 就被满足了。
现实世界
分布式系统是一个模拟系统。如果仅仅使用逻辑时钟,就相当于在使用一种系统内部自洽的方式对时间进行了模拟。由于逻辑时钟跟物理时间无关,因此我们站在系统内是不能感知到现实世界的时间流逝的。Alice 和 Bob 之所以能发现系统的时间戳产生异常,是因为他们之间存在一种系统外的信息传递方式。
假设我们生活在模拟系统内部,我们会发现,Bob在一个较早的逻辑时刻(对应较小的时间戳)接收到了来自Alice在较晚的逻辑时刻(对应较大的时间戳)的信息,相当于接收到了来自未来的信息,而且这个信息是通过不在这个系统内的某种机制传递的。据此,我们也许不需要特意“向外看”,就能推断出在这个系统外部,还有一个世界(我们的这个现实世界)。
同理,在我们当前生活的这个现实世界中,信息传递的速度受限于光速,而且时间永远向前流逝。也许某一天,我们发现了某种超越光速的信息传递手段,或者我们接收到了来自未来的信息(意味着我们可以预知未来了),那么,也许就说明,在我们这个世界的底层,还有一个更大的未知世界存在在那里。
总结
部分来自于网上
时间、时钟、事件顺序是三个不同的东西,现实中人们常常混淆,用时钟作为时间,用时间判断事件的前后顺序。但其实我们几乎无法获知物理时间,我们说的时间都是时钟,而时钟存在漂移,进而无法用于确定事件顺序。因此,需要用消息传递的方式来实现一个逻辑时钟,进而确定事件顺序。