Talk about Consistency and Consensus

ACID 中的一致性

我们现在关注的是其中的 C，即一致性 Consistency。它是什么意思呢？通俗地说，它指的是任何一个数据库事务的执行，都应该让整个数据库保持在「一致」的状态：

• ACID 中的「一致性」，是对于整个数据库的「一致」状态的维持。抽象来看，对数据库每进行一次事务操作，它的状态就发生一次变化。这相当于把数据库看成了状态机，只要数据库的起始状态是「一致」的，并且每次事务操作都能保持「一致性」，那么数据库就能始终保持在「一致」的状态上 (Consistency Preservation)。
• 所谓状态是不是「一致」，其实是由业务层规定的。比如转账的例子，“转账前后账户总额保持不变”，这个规定只对于「转账」这个特定的业务场景有效。如果换一个业务场景，「一致」的概念就不是这样规定了。所以说，ACID 中的「一致性」，其实是体现了业务逻辑上的合理性，并不是由数据库本身的技术特性所决定的。

为了让事务总是能保持 ACID 的一致性，我们需要在实现上考虑哪些因素呢？

• 出错情况 (failure/error)
  • 事务本身的实现逻辑可能存在错误，这需要应用层进行恰当的编码来保证。
  • 需要 ACID 中的 A（原子性）来保障。简言之，原子性保障了事务的执行要么全部成功，要么全部失败，而不允许出现“只执行了一半”这种“部分成功”的情况。
• 并发行为
  • 需要 ACID 中的 I（隔离性）来保障了。什么是隔离性呢？它对于并发执行的多个事务进行合理的排序，保障了不同事务的执行互不干扰。换言之，隔离性这种特性，能够让并发执行的多个事务就好像是按照「先后顺序」执行的一样。

Summary

• ACID 中的一致性，是个很偏应用层的概念。这跟 ACID 中的原子性、隔离性和持久性有很大的不同。原子性、隔离性和持久性，都是数据库本身所提供的技术特性；而一致性，则是由特定的业务场景规定的。
• 要真正做到 ACID 中的一致性，它是要依赖数据库的原子性和隔离性的（应对错误和并发）。
• 最后，ACID 中的一致性，甚至跟分布式都没什么直接关系。它跟分布式的唯一关联在于，在分布式环境下，它所依赖的数据库原子性和隔离性更难实现。

总之，ACID中的一致性，是一个非常特殊的概念。除了数据库事务处理，它很难扩展到其它场景，也跟分布式理论中的其它「一致性」概念没有什么关系。

分布式事务与共识算法的关系

共识问题 (consensus problem)。这是分布式系统中的一个十分基础而核心的问题，它表示如何在分布式系统中的多个节点之间就某事达成共识。

网上通常提到的「分布式一致性协议」，或者「分布式一致性算法」，一般来说就是解决这里的共识问题的算法。

这些算法或协议，经常包含 Paxos 之类，但也可能包括两阶段提交协议 (2 PC)或三阶段提交协议 (3 PC)。

ACID 中的原子性，要求事务的执行要么全部成功，要么全部失败，而不允许出现“部分成功”的情况。在分布式事务中，这要求参与事务的所有节点，要么全部执行 Commit 操作，要么全部执行 Abort 操作。换句话说，参与事务的所有节点，需要在“执行 Commit 还是 Abort”这一点上达成一致（其实就是共识）。这个问题在学术界被称为原子提交问题（Atomic Commitment Problem），而能够解决原子提交问题的算法，则被称为原子提交协议（Atomic Commitment Protocal，简称ACP）。2PC 和3PC，属于原子提交协议两种不同的具体实现。

我们可以发现原子提交问题和共识问题的关联：

• 共识问题，解决的是如何在分布式系统中的多个节点之间就某个提议达成共识。
• 原子提交问题，解决的是参与分布式事务的所有节点在“执行 Commit 还是 Abort”这一点上达成共识。
• 所以，原子提交问题是共识问题的一个特例。（？）

一些细节的不同，可能导致非常大的差异。当我们描述共识问题的时候，我们说的是在多个节点之间达成共识；而当我们描述原子提交问题的时候，我们说的是在所有节点之间达成共识。这个细微的差别，让这两类问题，几乎变成了完全不同的问题（谁也替代不了谁）：

• Paxos 协议为例，它只要求网络中的大部分节点达成共识就可以了，这样 Paxos 才能提供一定的容错性，只要网络中发生故障的节点不超过一半仍然能够正常工作（不会被阻塞）
• 对于解决原子提交问题的 2PC 或者 3PC 来说，即使只有一个节点发生故障了，其它节点也不能擅自决策进行 Commit 操作。所以，原子提交协议必须保证在参与分布式事务的所有节点（包括故障的节点）上对于“执行 Commit 还是 Abort”达成共识。

原子提交问题可以被抽象成一个新的一致性问题，称为 uniform consensus 问题，它是与通常的共识问题（consensus problem）不同的问题，而且是更难的问题。uniform consensus，要求所有节点（包括故障节点）都要达成共识；而 consensus 问题只关注没有发生故障的节点达成共识。

Summary

• 共识问题（consensus problem），解决的是如何在分布式系统中的多个节点之间就某个提议达成共识。它只关注没有发生故障的节点达成共识就可以了。
• 在分布式事务中，ACID 中的原子性，引出了原子提交问题，它解决的是参与分布式事务的所有节点在“执行 Commit 还是 Abort”这一点上达成共识。原子提交问题属于 uniform consensus 问题，要求所有节点（包括故障节点）都要达成共识，是比 consensus 问题更难的一类问题。
• Paxos 和解决拜占庭将军问题的算法，解决的是 consensus 问题；2PC/3PC，解决的是一个特定的 uniform consensus 问题。

CAP 与线性一致性

CAP 的三个字母分别代表了分布式系统的三个特性：一致性（Consistency）、可用性（Availability）和分区容错性（Partition-tolerance）。而 CAP 定理指出：任何一个分布式系统只能同时满足三个特性中的两个。但是，这一描述曾经引发了非常多的误解。

CAP 中的 C，也就是一致性，它是什么意思呢？在证明 CAP 定理的原始论文中，C 指的是 linearizable consistency，也就是「线性一致性」。更精简的英文表达则是 linearizability。

线性一致性（linearizability）是 CAP 中的 C 的原始定义。而很多人在谈到 CAP 时，则会把这个 C 看成是强一致性（strong consistency）。这其实也没错，因为线性一致性的另一个名字，就是强一致性。

所以线性一致性是什么意思呢？

大体上是说，在一个并发执行的环境中，不同的操作之间可能是有严格的先后关系的（一个操作执行结束之后另一个操作才开始执行），也可能是并发执行的（一个操作还没执行结束，另一个操作就开始执行了）；如果能够把所有操作排列成一个「合法」的全局线性顺序，那么这些操作就是满足线性一致性的。当然，在这个重新排列的过程中，原来就存在的严格的先后关系，必须得以保持。

对于一个分布式存储系统来说，线性一致性的含义可以用一个具体的描述来取代：对于任何一个数据对象来说，系统表现得就像它只有一个副本一样。

一致性模型的来历

我们之所以使用分布式系统，无非是因为分布式系统能带来一些「好处」，比如容错性、可扩展性等等。为了获得这些「好处」，分布式系统实现上常用的方法是复制 (replication) 和分片 (sharding)。而我们将要讨论的一致性模型 (consistency model)，主要是与复制有关。

复制带来的具体「好处」主要是体现在两个方面：

• 容错 (fault tolerance)。即使某些网络节点发生故障，由于原本保存着在故障节点上的数据在正常节点上还有备份，所以整个系统仍然可能是可用的。这也是我们期待分布式系统能够提供的「高可用」特性。
• 提升吞吐量。将一份数据复制多份并保存在多个副本节点上，还顺便带来一个好处：对于同一个数据对象的访问请求（至少是读请求）可以由多个副本节点分担，从而使得整个系统可以随着请求量的增加不断扩展。

而复制带来的最大的挑战就是数据一致性问题。严格意义上来说，让所有副本在任何时刻都保持一致是不可能的，因为副本之间的数据同步是需要时间的。但是只要系统能够保证，每当我们去「观察」的时候（即读取数据副本的时候），系统表现出来的行为是一致的，就可以了。

所以我们应该从系统用户（使用系统的开发者）的角度来对数据一致性的要求进行定义。

讨论一个例子：用户 A 先在第1个副本上执行 x=42，然后用户 B 再在第2个副本上执行 x=43，最后用户 C 在第3个副本上读取_x_的值。仍然为了让系统“表现得像只有一个副本”，直觉上看，用户 C 读取到的_x_的值似乎应该是43。但是，也不一定非要如此。因为两个写操作是分别由用户 A 和用户 B 发起的，他们并不知道彼此谁先谁后（虽然从时间上看用户 A 的写操作确实在先）。所以，我们也可以选择认为用户 B 执行 x=43在用户 A 执行 x=42之前。这样的话，用户 C 读取到的 x 的值就应该是42。（这种排序满足顺序一致性，但不满足线性一致性。）

一个系统在数据一致性上的具体表现如何，取决于系统对关键事件（读写操作）的排序和执行采取什么样的规则和限制。比如在上述的例子中，虽然两种排序结果不同，但它们都做到了让系统“表现得像只有一个副本”。它们的不同在于，前一种排序遵循了不同用户的操作的时间先后顺序，而后一种排序没有。

一个分布式系统对于读写操作的某种排序和执行规则，就定义了一种一致性模型 (consistency model)。当一个系统选定了某种特定的一致性模型（比如线性一致性或顺序一致性），那么你就只能看到这种一致性模型所允许的那些操作序列。

顺序一致性和线性一致性

• 顺序一致性：sequential consistency
• 线性一致性：linearizability

顺序一致性

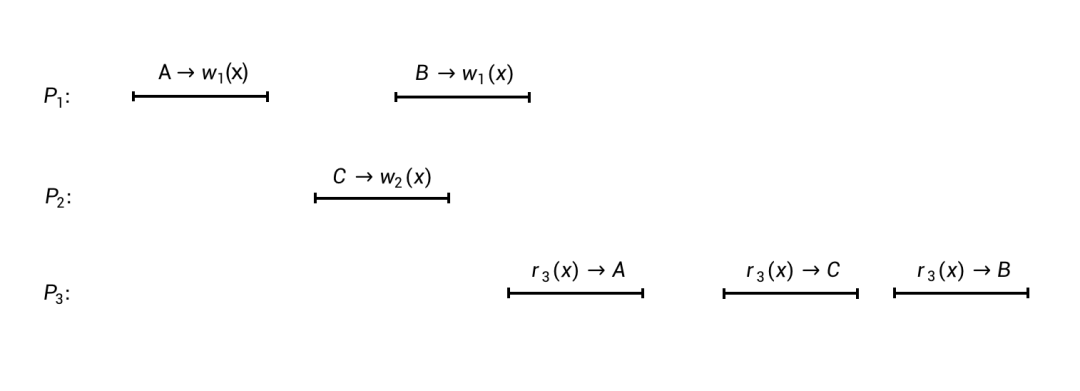
• A –> w_i(x)，表示一个写操作：第 i 个进程向数据对象 x 写入了值 A。
• r_i(x) –> A，表示一个读操作：第 i 个进程从数据对象 x 中读到了值 A。

上图的这样一个执行过程，是否满足顺序一致性？

顺序一致性定义：如果一个并发执行过程所包含的所有读写操作能够重排成一个全局线性有序的序列，并且这个序列满足以下两个条件，那么这个并发执行过程就是满足顺序一致性的：

• 条件I：重排后的序列中每一个读操作返回的值，必须等于前面对同一个数据对象的最近一次写操作所写入的值。
• 条件 II：原来每个进程中各个操作的执行先后顺序，在这个重排后的序列中必须保持一致。

简单重排一下：

1. 写 A
2. 读 A
3. 写 C
4. 读 C
5. 写 B
6. 读 B

这个序列是满足顺序一致性的两个条件的，所以上图的执行过程是满足顺序一致性的。

为什么顺序一致性会这样定义呢？

首先，重排成一个全局线性有序的序列，相当于系统对外表现出了一种「假象」，原本多进程并发执行的操作，好像是顺序执行的一样。顺序一致性正是遵循了这种「系统假象」，系统对外表现就好像在操作一个单一的副本，执行顺序也必然是可以看做顺序执行的：

• 条件 I 规定了系统的表现是合理的（即合乎逻辑的）；
• 条件 II 则保证了以任何进程的视角来看，它所发起的操作执行顺序都是符合它原本的预期的。

总之，一个满足顺序一致性的系统，对外表现就好像总是在操作一个副本一样。

下图是一个不满足顺序一致性的例子：

线性一致性

线性一致性的定义，与顺序一致性非常相似，也是试图把所有读写操作重排成一个全局线性有序的序列，但除了满足前面的条件 I 和条件 II 之外，还要同时满足一个条件：

• 条件 III：不同进程的操作，如果在时间上不重叠，那么它们的执行先后顺序，在这个重排后的序列中必须保持一致。

所以下图这个例子是不满足线性一致性的：

C 已经成功写入了，P_3 的第一次读是不会读到 A 的。

下图是满足线性一致性的：

重排后一个有效的序列是：

1. 写 A
2. 读 A
3. 写 C
4. 读 C
5. 写 B
6. 读 B

现在我们可以仔细分析一下条件 II 和条件 III，它们囊括了任意两个操作之间所有可能的先后关系：

• 进程内的任意两个操作之间，总是先后顺序执行的（执行时间上不可能重叠）；而根据条件II，它们的先后顺序在最后重排后的序列中也会保持。
• 不同进程的不同操作之间，在执行时间上可能重叠（并发执行），也可能不重叠。根据条件 III，不重叠的两个操作，它们在时间上的先后顺序，在最后重排后的序列中会得以保持。而对于执行时间上重叠的两个操作，它们在最后重排后的序列中的先后顺序没有规定。

Summary

• 线性一致性隐含了时效性保证（recency guarantee）。它保证我们总是能读到数据最新的值。
• 在顺序一致性中，我们有可能读到旧版本的数据。

最终一致性

系统维持强一致性是有成本的。想要维持越强的一致性，就需要在副本节点之间做更多的通信和协调工作，因此会降低操作的总延迟，进而降低整个系统的性能。

从20世纪90年代中期开始，互联网开始蓬勃发展，系统的规模也变得越来越大。人们设计大型分布式系统的指导思想，也逐步开始更倾向于系统的高可用性和高性能。取舍的结果就是，降低系统提供的一致性保障。这其中非常重要的一条思路就是最终一致性。

最终一致性的定义如下：

Eventual consistency. This is a specific form of weak consistency; the storage system guarantees that if no new updates are made to the object, eventually all accesses will return the last updated value. 最终一致性是弱一致性的一种特殊形式；存储系统保证，如果对象没有新的修改操作，那么所有的访问最终都会返回最新写入的值。

虽然最终一致性和本文前面讨论的线性一致性或顺序一致性在命名上非常相似，但它的定义却与后两者存在非常大的差别。深层的原因在于，它们其实属于不同类别的系统属性 (property)。

• 线性一致性和顺序一致性属于 safety property（安全性）；
• 最终一致性属于 liveness property（活性）

实际上，最终一致性有点名不副实，它更好的名字可能是收敛性 (convergence)，表示所有副本最终都会收敛到相同的值。

一致性的强弱关系

一致性模型的强弱关系，其实是有更严格的定义的：

• 当且仅当一个一致性模型所能接受的执行过程，都能被另一个一致性模型所接受时（前者的集合是后者集合的子集），我们就说前者是比后者「更强」(stronger) 的一致性模型。

仔细分析一下也能知道，一致性模型的强弱关系定义，是基于 safety 属性定义的。所以，将线性一致性或顺序一致性与最终一致性比较强弱，这并不是一个严格的做法。实际上，就像我们前一小节所讨论的，最终一致性在 safety 方面提供的保证为零，它是属于 liveness 的概念。一个系统可以在提供最终一致性的同时，也提供另外一种更强一点的带有 safety 属性的一致性（比如因果一致性）。