DDIA: Chapter 8 The Trouble with Distributed Systems

Faults and Partial Failures

An individual computer with good software is usually either fully functional or entirely broken, but not something in between. Thus, computers hide the fuzzy physical reality on which they are implemented and present an idealized system model that operates with mathematical perfection.

In a distributed system, there may well be some parts of the system that are broken in some unpredictable way, even though other parts of the system are working fine. This is known as a partial failure. The difficulty is that partial failures are nondeterministic: if you try to do anything involving multiple nodes and the network, it may sometimes work and sometimes unpredictably fail.

Unreliable Networks

Network Faults in Practice

Handling network faults doesn’t necessarily mean tolerating them: if your network is normally fairly reliable, a valid approach may be to simply show an error message to users while your network is experiencing problems.

Detecting Faults

Unfortunately, the uncertainty about the network makes it difficult to tell whether a node is working or not.

You can retry a few times (TCP retries transparently, but you may also retry at the application level), wait for a timeout to elapse, and eventually declare the node dead if you don’t hear back within the timeout.

Timeouts and Unbounded Delays

Imagine a fictitious system with a network that guaranteed a maximum delay for packets—every packet is either delivered within some time d, or it is lost, but delivery never takes longer than d. Furthermore, assume that you can guarantee that a nonfailed node always handles a request within some time r. In this case, you could guarantee that every successful request receives a response within time 2 d + r—and if you don’t receive a response within that time, you know that either the network or the remote node is not working. If this was true, 2 d + r would be a reasonable timeout to use.

Unfortunately, most systems we work with have neither of those guarantees: asynchronous networks have unbounded delays (that is, they try to deliver packets as quickly as possible, but there is no upper limit on the time it may take for a packet to arrive), and most server implementations cannot guarantee that they can handle requests within some maximum time.

Network congestion and queueing

The variability of packet delays on computer networks is most often due to queueing:

• If there is so much incoming data that the switch queue fills up, the packet is dropped, so it needs to be resent—even though the network is functioning fine.
• When a packet reaches the destination machine, if all CPU cores are currently busy, the incoming request from the network is queued by the operating system until the application is ready to handle it.
• TCP performs flow control, in which a node limits its own rate of sending in order to avoid overloading a network link or the receiving node.

Synchronous Versus Asynchronous Networks

Why do datacenter networks and the internet use packet switching? The answer is that they are optimized for bursty traffic.

With careful use of quality of service (QoS, prioritization and scheduling of packets) and admission control (rate-limiting senders), it is possible to emulate circuit switching on packet networks, or provide statistically bounded delay.

However, currently deployed technology does not allow us to make any guarantees about delays or reliability of the network: we have to assume that network congestion, queueing, and unbounded delays will happen. Consequently, there’s no “correct” value for timeouts—they need to be determined experimentally.

Unreliable Clocks

This fact sometimes makes it difficult to determine the order in which things happened when multiple machines are involved.

Monotonic Versus Time-of-Day Clocks

Modern computers have at least two different kinds of clocks: a time-of-day clock and a monotonic clock. Although they both measure time, it is important to distinguish the two, since they serve different purposes.

Time-of-day clocks

A time-of-day clock does what you intuitively expect of a clock: it returns the current date and time according to some calendar.

For example, clock_gettime(CLOCK_REALTIME) on Linux.

Time-of-day clocks are usually synchronized with NTP, which means that a timestamp from one machine (ideally) means the same as a timestamp on another machine. In particular, if the local clock is too far ahead of the NTP server, it may be forcibly reset and appear to jump back to a previous point in time. These jumps, as well as the fact that they often ignore leap seconds, make time-of-day clocks unsuitable for measuring elapsed time.

Monotonic clocks

A monotonic clock is suitable for measuring a duration (time interval), such as a timeout or a service’s response time: clock_gettime(CLOCK_MONOTONIC) on Linux and System.NanoTime() in Java are monotonic clocks, for example.

The name comes from the fact that they are guaranteed to always move forward (whereas a time-of-day clock may jump back in time).

In a distributed system, using a monotonic clock for measuring elapsed time (e.g., timeouts) is usually fine, because it doesn’t assume any synchronization between different nodes’ clocks and is not sensitive to slight inaccuracies of measurement.

Clock Synchronization and Accuracy

Monotonic clocks don’t need synchronization, but time-of-day clocks need to be set according to an NTP server or other external time source in order to be useful.

Our methods for getting a clock to tell the correct time aren’t nearly as reliable or accurate as you might hope：

• The quartz clock in a computer is not very accurate: it drifts (runs faster or slower than it should).
• If a computer’s clock differs too much from an NTP server, it may refuse to synchronize, or the local clock will be forcibly reset。
• NTP synchronization can only be as good as the network delay, so there is a limit to its accuracy when you’re on a congested network with variable packet delays.
• Leap seconds result in a minute that is 59 seconds or 61 seconds long, which messes up timing assumptions in systems that are not designed with leap seconds in mind.
• In virtual machines, the hardware clock is virtualized, which raises additional challenges for applications that need accurate timekeeping.

Relying on Synchronized Clocks

The problem with clocks is that while they seem simple and easy to use, they have a surprising number of pitfalls:

• A day may not have exactly 86,400 seconds.
• Time-of-day clocks may move backward in time.
• The time on one node may be quite different from the time on another node.

Timestamps for ordering events

Let’s consider one particular situation in which it is tempting, but dangerous, to rely on clocks: ordering of events across multiple nodes. For example, if two clients write to a distributed database, who got there first?

The write x = 1 has a timestamp of 42.004 seconds, but the write x = 2 has a timestamp of 42.003 seconds, even though x = 2 occurred unambiguously later. When node 2 receives these two events, it will incorrectly conclude that x = 1 is the more recent value and drop the write x = 2. In effect, client B’s increment operation will be lost.

This conflict resolution strategy is called last write wins (LWW), and it is widely used in both multi-leader replication and leaderless databases.

• Database writes can mysteriously disappear: a node with a lagging clock is unable to overwrite values previously written by a node with a fast clock until the clock skew between the nodes has elapsed.
• LWW cannot distinguish between writes that occurred sequentially in quick succession.
• It is possible for two nodes to independently generate writes with the same timestamp, especially when the clock only has millisecond resolution.

Could NTP synchronization be made accurate enough that such incorrect orderings cannot occur? Probably not, because NTP’s synchronization accuracy is itself limited by the network round-trip time, in addition to other sources of error such as quartz drift. For correct ordering, you would need the clock source to be significantly more accurate than the thing you are measuring (namely network delay).

这种时候逻辑时钟就能派上用场了，还是上面的那种情况：

因为 set x=1 和 increase x+=1 是有因果关系的，所以用 Happened Before 这种关系维护的全局排序是能反映这两个操作的因果关系的（increase x+=1 的时间戳一定大于 set x=1，因为在 N3 里它后于 set x=1 发生）。

Clock readings have a confidence interval

“置信区间”

The uncertainty bound can be calculated based on your time source. If you have a GPS receiver or atomic (caesium) clock directly attached to your computer, the expected error range is reported by the manufacturer. If you’re getting the time from a server, the uncertainty is based on the expected quartz drift since your last sync with the server, plus the NTP server’s uncertainty, plus the network round-trip time to the server (to a first approximation, and assuming you trust the server).

Unfortunately, most systems don’t expose this uncertainty: for example, when you call clock_gettime(), the return value doesn’t tell you the expected error of the timestamp, so you don’t know if its confidence interval is five milliseconds or five years.

Synchronized clocks for global snapshots

The most common implementation of snapshot isolation requires a monotonically increasing transaction ID. If a write happened later than the snapshot (i.e., the write has a greater transaction ID than the snapshot), that write is invisible to the snapshot transaction.

However, when a database is distributed across many machines, potentially in multiple datacenters, a global, monotonically increasing transaction ID (across all partitions) is difficult to generate, because it requires coordination.

Spanner implements snapshot isolation across datacenters in this way. It uses the clock’s confidence interval as reported by the TrueTime API, and is based on the following observation: if you have two confidence intervals, each consisting of an earliest and latest possible timestamp (A = [Aearliest, Alatest] and B = [Bearliest, Blatest]), and those two intervals do not overlap (i.e., Aearliest < Alatest < Bearliest < Blatest), then B definitely happened after A—there can be no doubt. Only if the intervals overlap are we unsure in which order A and B happened.

Using clock synchronization for distributed transaction semantics is an area of active research. These ideas are interesting, but they have not yet been implemented in mainstream databases outside of Google.

Process Pauses

while (true) { 
 request = getIncomingRequest(); 
 // Ensure that the lease always has at least 10 seconds remaining 
 if (lease.expiryTimeMillis - System.currentTimeMillis() < 10000) {
  lease = lease.renew(); 
 } 
 if (lease.isValid()) { 
  process(request); 
 } 
}

What’s wrong with this code?

Firstly, it’s relying on synchronized clocks: the expiry time on the lease is set by a different machine (where the expiry may be calculated as the current time plus 30 seconds, for example), and it’s being compared to the local system clock. If the clocks are out of sync by more than a few seconds, this code will start doing strange things.

Secondly, even if we change the protocol to only use the local monotonic clock, there is another problem: the code assumes that very little time passes between the point that it checks the time (System.CurrentTimeMillis()) and the time when the request is processed (process (request)).

Is it crazy to assume that a thread might be paused for so long? Unfortunately not. There are various reasons why this could happen:

• Many programming language runtimes (such as the Java Virtual Machine) have a garbage collector (GC) that occasionally needs to stop all running threads. These “stop-the-world” GC pauses have sometimes been known to last for several minutes.
• In virtualized environments, a virtual machine can be suspended (pausing the execution of all processes and saving the contents of memory to disk) and resumed (restoring the contents of memory and continuing execution).
• If the application performs synchronous disk access, a thread may be paused waiting for a slow disk I/O operation to complete.
• If the operating system is configured to allow swapping to disk (paging), a simple memory access may result in a page fault that requires a page from disk to be loaded into memory. The thread is paused while this slow I/O operation takes place.

You can’t assume anything about timing, because arbitrary context switches and parallelism may occur.

Limiting the impact of garbage collection

An emerging idea is to treat GC pauses like brief planned outages of a node, and to let other nodes handle requests from clients while one node is collecting its garbage.

A variant of this idea is to use the garbage collector only for short-lived objects (which are fast to collect) and to restart processes periodically, before they accumulate enough long-lived objects to require a full GC of long-lived objects.

Knowledge, Truth, and Lies

So far in this chapter we have explored the ways in which distributed systems are different from programs running on a single computer: there is no shared memory, only message passing via an unreliable network with variable delays, and the systems may suffer from partial failures, unreliable clocks, and processing pauses.

The Truth Is Defined by the Majority

A distributed system cannot exclusively rely on a single node, because a node may fail at any time, potentially leaving the system stuck and unable to recover. Instead, many distributed algorithms rely on a quorum, that is, voting among the nodes: decisions require some minimum number of votes from several nodes in order to reduce the dependence on any one particular node.

The leader and the lock

Frequently, a system requires there to be only one of some thing:

• Only one node is allowed to be the leader for a database partition, to avoid split brain.
• Only one transaction or client is allowed to hold the lock for a particular resource or object, to prevent concurrently writing to it and corrupting it.
• Only one user is allowed to register a particular username, because a username must uniquely identify a user.

Below shows a data corruption bug due to an incorrect implementation of locking:

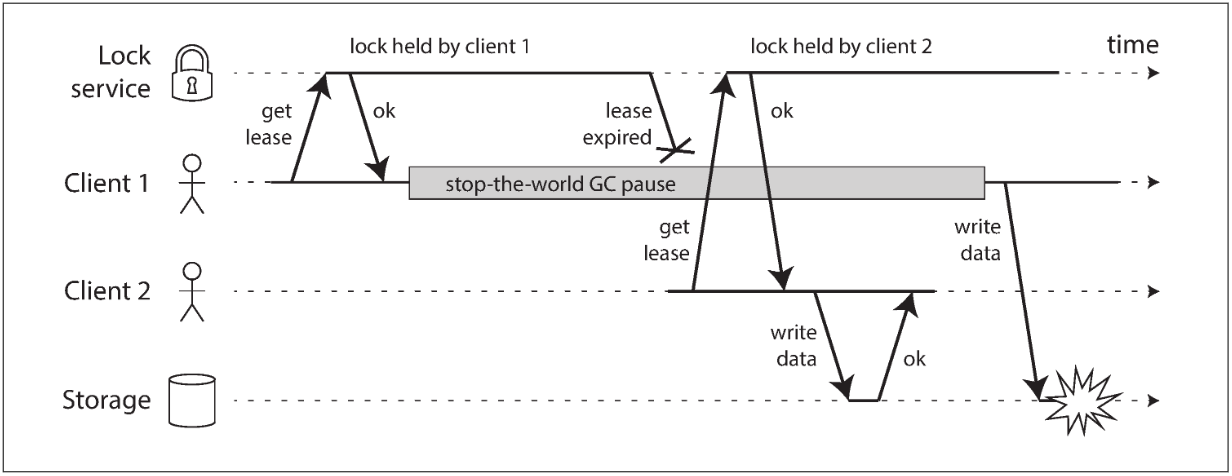
If the client holding the lease is paused for too long, its lease expires. Another client can obtain a lease for the same file, and start writing to the file. When the paused client comes back, it believes (incorrectly) that it still has a valid lease and proceeds to also write to the file.

Fencing tokens

When using a lock or lease to protect access to some resource, we need to ensure that a node that is under a false belief of being “the chosen one” cannot disrupt the rest of the system. A fairly simple technique that achieves this goal is called fencing:

This approach is under arguments:

Distributed locks are very useful exactly when we have no other control in the shared resource.

If ZooKeeper is used as lock service, the transaction ID zxid or the node version cversion can be used as fencing token. Since they are guaranteed to be monotonically increasing, they have the required properties.

Byzantine Faults

Distributed systems problems become much harder if there is a risk that nodes may “lie” (send arbitrary faulty or corrupted responses)—for example, if a node may claim to have received a particular message when in fact it didn’t. Such behavior is known as a Byzantine fault, and the problem of reaching consensus in this untrusting environment is known as the Byzantine Generals Problem.

A system is Byzantine fault-tolerant if it continues to operate correctly even if some of the nodes are malfunctioning and not obeying the protocol, or if malicious attackers are interfering with the network.

A bug in the software could be regarded as a Byzantine fault, but if you deploy the same software to all nodes, then a Byzantine fault-tolerant algorithm cannot save you. Most Byzantine fault-tolerant algorithms require a supermajority of more than twothirds of the nodes to be functioning correctly (i.e., if you have four nodes, at most one may malfunction).

System Model and Reality

Algorithms need to be written in a way that does not depend too heavily on the details of the hardware and software configuration on which they are run. This in turn requires that we somehow formalize the kinds of faults that we expect to happen in a system.

We do this by defining a system model, which is an abstraction that describes what things an algorithm may assume.

With regard to timing assumptions, three system models are in common use:

• Synchronous model
  • The synchronous model assumes bounded network delay, bounded process pauses, and bounded clock error.
  • This does not imply exactly synchronized clocks or zero network delay; it just means you know that network delay, pauses, and clock drift will never exceed some fixed upper bound.
• Partially synchronous model
  • Partially synchronous model Partial synchrony means that a system behaves like a synchronous system most of the time, but it sometimes exceeds the bounds for network delay, process pauses, and clock drift.
  • This is a realistic model of many systems: most of the time, networks and processes are quite well behaved—otherwise we would never be able to get anything done—but we have to reckon with the fact that any timing assumptions may be shattered occasionally.
• Asynchronous model
  • asynchronous model In this model, an algorithm is not allowed to make any timing assumptions — in fact, it does not even have a clock (so it cannot use timeouts).

Moreover, besides timing issues, we have to consider node failures. The three most common system models for nodes are:

• Crash-stop faults
  • In the crash-stop model, an algorithm may assume that a node can fail in only one way, namely by crashing.
• Crash-recovery faults
  • We assume that nodes may crash at any moment, and perhaps start responding again after some unknown time. In the crash-recovery model, nodes are assumed to have stable storage (i.e., nonvolatile disk storage) that is preserved across crashes, while the in-memory state is assumed to be lost.
• Byzantine (arbitrary) faults
  • Nodes may do absolutely anything, including trying to trick and deceive other nodes.

For modeling real systems, the partially synchronous model with crash-recovery faults is generally the most useful model.

Correctness of an algorithm

To define what it means for an algorithm to be correct, we can describe its properties.

For example, the output of a sorting algorithm has the property that for any two distinct elements of the output list, the element further to the left is smaller than the element further to the right.

Safety and liveness

To clarify the situation, it is worth distinguishing between two different kinds of properties: safety and liveness properties.

What distinguishes the two kinds of properties? A giveaway is that liveness properties often include the word “eventually” in their definition. (And yes, you guessed it - eventual consistency is a liveness property.)

Safety is often informally defined as nothing bad happens, and liveness as something good eventually happens.

The actual definitions of safety and liveness are precise and mathematical:

• If a safety property is violated, we can point at a particular point in time at which it was broken. After a safety property has been violated, the violation cannot be undone—the damage is already done.
• A liveness property works the other way round: it may not hold at some point in time. There is always hope that it may be satisfied in the future (namely by receiving a response).

An advantage of distinguishing between safety and liveness properties is that it helps us deal with difficult system models.

For distributed algorithms, it is common to require that safety properties always hold, in all possible situations of a system model. That is, even if all nodes crash, or the entire network fails, the algorithm must nevertheless ensure that it does not return a wrong result (i.e., that the safety properties remain satisfied).

However, with liveness properties we are allowed to make caveats: for example, we could say that a request needs to receive a response only if a majority of nodes have not crashed, and only if the network eventually recovers from an outage. The definition of the partially synchronous model requires that eventually the system returns to a synchronous state—that is, any period of network interruption lasts only for a finite duration and is then repaired.