For self reference.

Forward Pass

“forward pass” (前向传播) 是指神经网络从输入数据开始，逐层计算，直到产生最终输出（预测结果）的过程。可以把它想象成信息在网络中“向前流动”的过程。

与前向传播相对应的，确实还有一个非常关键的步骤叫做 “backward pass” (反向传播)，通常更准确地称为 反向传播算法 (Backpropagation)

Backward Pass 的作用：

  1. 计算损失 (Calculate Loss):

    • 在前向传播得到预测值 a 之后，我们会将它与真实的标签 y (在你的代码中是 torch.tensor([1.0])) 进行比较，计算出一个“损失值” (loss)。
    • 你的代码中 loss = F.binary_cross_entropy(a, y) 做的就是这件事。binary_cross_entropy 是一种常用的损失函数，用于衡量二分类问题中预测值和真实值之间的差异。损失值越小，说明模型的预测越准确。

  2. 计算梯度 (Calculate Gradients):

    • 反向传播的核心任务是计算损失函数相对于模型中每个参数（在你的例子中是 w1 和 b）的梯度 (gradient)。
    • 梯度可以告诉我们：为了减小损失，每个参数应该向哪个方向调整，以及调整的幅度有多大。简单来说，梯度指向了损失函数增长最快的方向，所以我们会沿着梯度的反方向去调整参数，以期减小损失。

  3. 更新参数 (Update Parameters):

    • 根据计算得到的梯度，使用一种叫做优化器 (optimizer) (例如 SGD, Adam 等) 的算法来更新模型的参数 (w1 和 b)。
    • 目标是让模型在下一次进行前向传播时，能做出更准确的预测，从而得到更小的损失

得到 loss 之后, 可以通过链式法则得到模型中每个参数的梯度, 为了最小化 loss, 最基本的参数更新规则是梯度下降法。对于每个参数，更新规则如下:

new_parameter = old_parameter - learning_rate * gradient

虽然基础的梯度下降法很简单，但在实践中，研究人员发现了很多更高级、更有效的优化算法(Optimizer):

  • SGD (Stochastic Gradient Descent) with Momentum: 借用了物理学中“动量”的概念。如果梯度连续指向同一个方向，参数更新的步长会逐渐加速；如果梯度方向改变，动量会帮助减缓更新，有助于跳出局部最小值或平坦区域。
  • AdaGrad (Adaptive Gradient Algorithm): 为不同的参数自动调整学习率。对于不经常更新的参数，它会使用较大的学习率；对于经常更新的参数，它会使用较小的学习率。
  • RMSprop (Root Mean Square Propagation): 也是一种自适应学习率的方法，是 AdaGrad 的改进，解决了其学习率可能过早衰减到零的问题。
  • Adam (Adaptive Moment Estimation): 被广泛使用，它结合了 Momentum 和 RMSprop 的优点，通常能快速收敛且效果良好。

参数更新完成后，一次“前向传播 -> 计算损失 -> 计算梯度 -> 更新参数”的完整迭代就结束了。然后，模型会带着更新后的参数，在下一批数据（或者同样的数据）上重复这个过程。

梯度是损失函数相对于当前参数值的导数： 梯度（$\dfrac{\partial \text{Loss}}{\partial w}$）衡量的是，在当前权重 w 的取值下，如果 w 发生微小变化，损失 Loss 会如何变化。

在下一次迭代开始时，权重 w 的值已经和上一次迭代时不同

链式法则的核心思想: 某一点（或参数）的最终梯度 = 上游传来的梯度 × 经过该点的局部梯度

计算图是一个 DAG

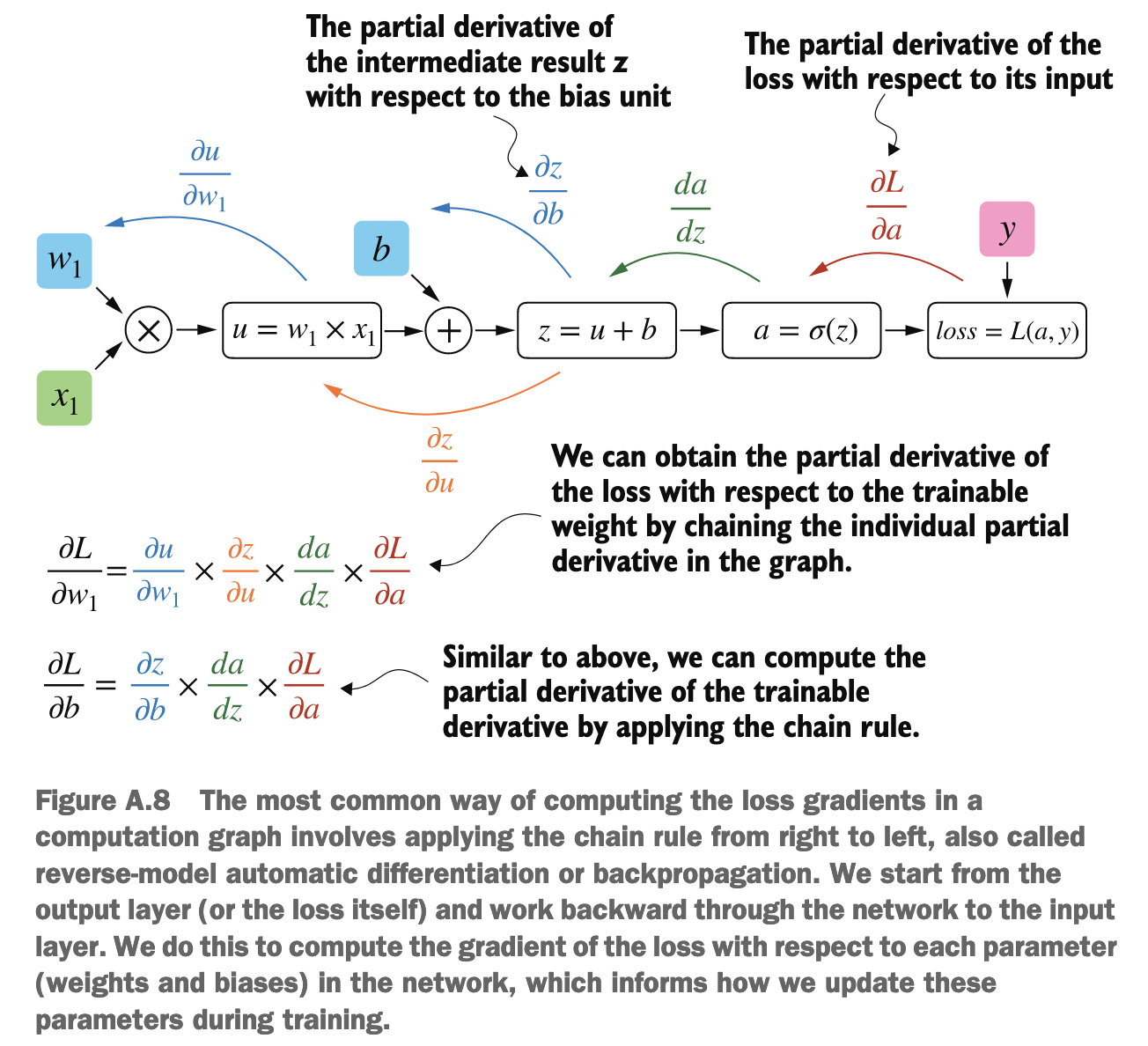
pasted-image-20250521103904.png

反向传播就可以直接利用上一步的结果进行下一步的计算, 有一点像记忆化搜索

Summary

On a high level, all you need to know for this book is that the chain rule is a way to compute gradients of a loss function given the model’s parameters in a computation graph.

  • 多变量函数 (Multivariate function)：就是一个有多个输入变量的函数。在深度学习中，损失函数通常是多变量函数，它的输入是模型的所有权重（weights）和偏置（biases）。
  • 梯度 (Gradient)：梯度是一个向量 (vector)。这个向量的特殊之处在于，它的每一个分量（component）都是该多变量函数相对于其某一个输入变量的偏导数。

如果一个损失函数 $L$ 取决于很多权重 $w_1, w_2, …, w_n$ 和偏置 $b_1, b_2, …, b_m$，那么损失函数 $L$ 的梯度就是一个包含所有这些偏导数的向量：

$$\nabla L = \left( \frac{\partial L}{\partial w_1}, \frac{\partial L}{\partial w_2}, …, \frac{\partial L}{\partial w_n}, \frac{\partial L}{\partial b_1}, \frac{\partial L}{\partial b_2}, …, \frac{\partial L}{\partial b_m} \right)$$ 这是一个 $(n+m)$ 维的向量

Multilayer Neural Networks

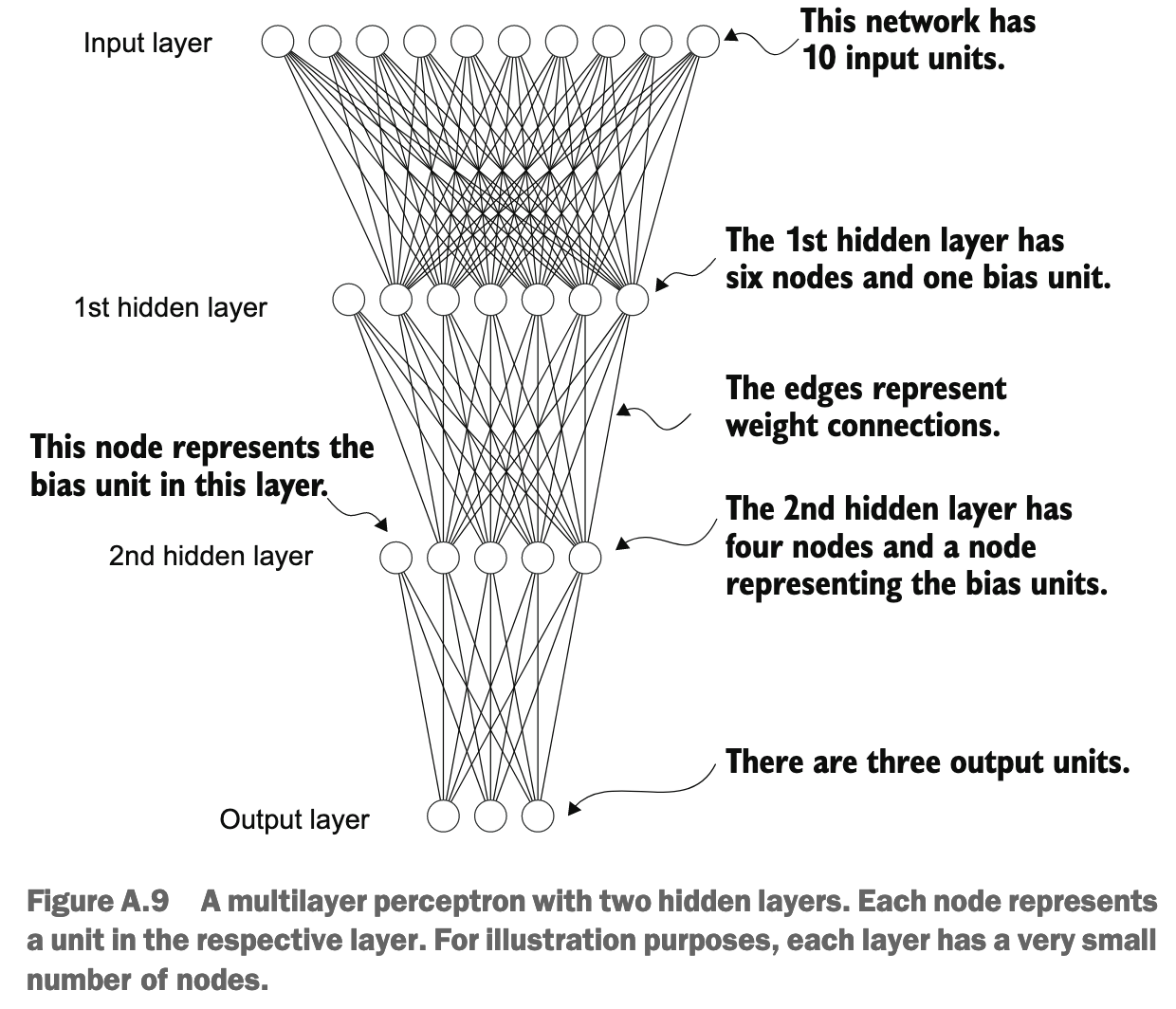
pasted-image-20250521110333.png

import torch
import torch.nn as nn

class NeuralNetwork(nn.Module):
    def __init__(self, num_inputs, num_outputs):
        super().__init__()
        self.layers = nn.Sequential(
            # 1st hidden layer
            nn.Linear(num_inputs, 30),
            nn.ReLU(),
            # 2nd hidden layer
            nn.Linear(30, 20),
            nn.ReLU(),
            # Output layer
            nn.Linear(20, num_outputs),
        )

    def forward(self, x):
        logits = self.layers(x)
        return logits
  • torch.nn.Linear 代表一个全连接层（fully connected layer），这个单元（或层）对其输入执行一个线性变换

执行线性变换：它将输入的 in_features 通过一个权重矩阵 W 和一个偏置向量 b 转换成 out_features。数学表达式为：

$$ output=input \cdot W^T+b $$

其中：

  • input 是输入张量
  • W 是一个形状为 (out_features, in_features) 的权重矩阵。这是该层学习的参数之一。
  • b 是一个形状为 (out_features) 的偏置向量。这也是该层学习的参数之一
  • $W^T$ 表示权重矩阵 W 的转置

分解一下各个部分的维度：

  1. input (输入张量):
    • 通常，输入是一个批次 (batch) 的数据。如果每个输入样本有 in_features 个特征，并且批次大小为 batch_size，那么 input 的形状是 (batch_size, in_features)。
    • 为了简单起见，我们先考虑单个输入样本，可以看作一个行向量，形状为 (1, in_features)。
  2. W (权重矩阵，PyTorch中 nn.Linear 层的 weight 参数):
    • 在 PyTorch 的 nn.Linear(in_features, out_features) 层中，其内部存储的权重矩阵 self.weight（我们在这里称之为 W）的形状是 (out_features, in_features)。
    • 这个形状的含义是：它有 out_features 行，每一行对应一个输出神经元的权重；它有 in_features 列，每一列对应一个输入特征的权重
  3. b (偏置向量):
    • 形状是 (out_features)。在进行加法时，它会被广播（broadcast）以匹配输出的形状。
  4. output (输出张量):
    • 我们期望的输出形状是 (batch_size, out_features)（或者对于单个样本，是 (1, out_features)）

在 PyTorch 中，推荐模型直接输出 logits，然后使用像 torch.nn.CrossEntropyLoss 或 torch.nn.BCEWithLogitsLoss 这样的损失函数。这样做的好处是：

  1. 代码更简洁：你不需要在模型中显式添加 Softmax 或 Sigmoid 层（除非你确实需要在模型输出概率值用于其他目的，比如在推理时）。
  2. 训练更稳定：结合的损失函数内部使用了数值技巧来避免计算过程中可能出现的上溢或下溢问题。
  3. 计算更高效：合并的操作通常经过优化，运行速度更快。

Data Loaders

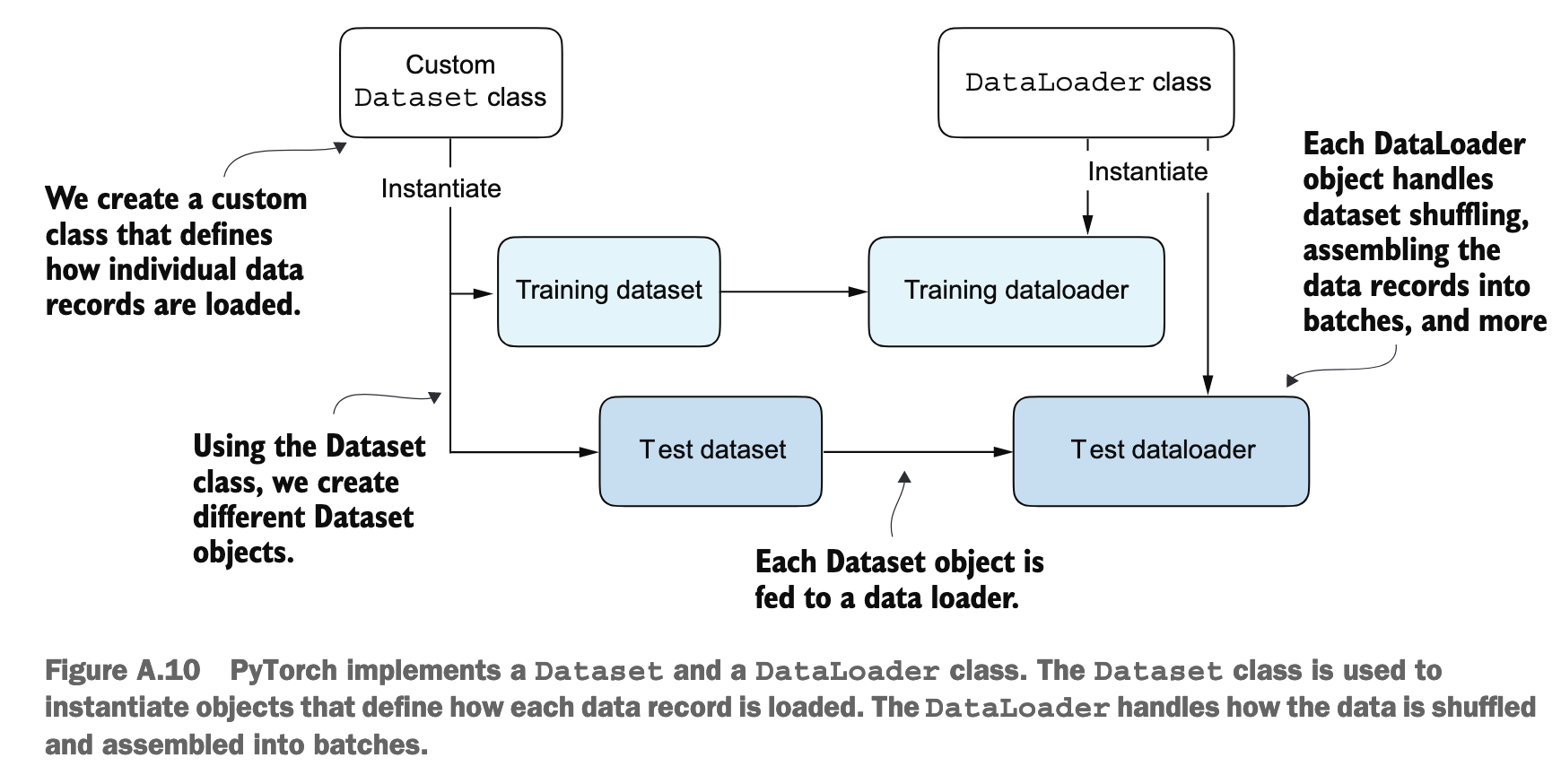
pasted-image-20250521152427.png

import torch
from torch.utils.data import Dataset, DataLoader

class ToyDataset(Dataset):
    def __init__(self, X, y):
        self.features = X
        self.labels = y

    def __getitem__(self, index):
        one_x = self.features[index]
        one_y = self.labels[index]
        return one_x, one_y

    def __len__(self):
        return self.labels.shape[0]


torch.manual_seed(123)

train_loader = DataLoader(
    dataset=train_ds,
    batch_size=2,
    shuffle=True,
    num_workers=0
)

test_loader = DataLoader(
    dataset=test_ds,
    batch_size=2,
    shuffle=False,
    num_workers=0
)
  • 在数据科学和机器学习中，通常约定数组/张量的第一个维度代表样本的数量
  • 当 num_workers 被设为 0 时，意味着所有的数据加载操作都将在主进程中串行执行
  • 可以加上 drop_last=True 来避免不完整的 batch

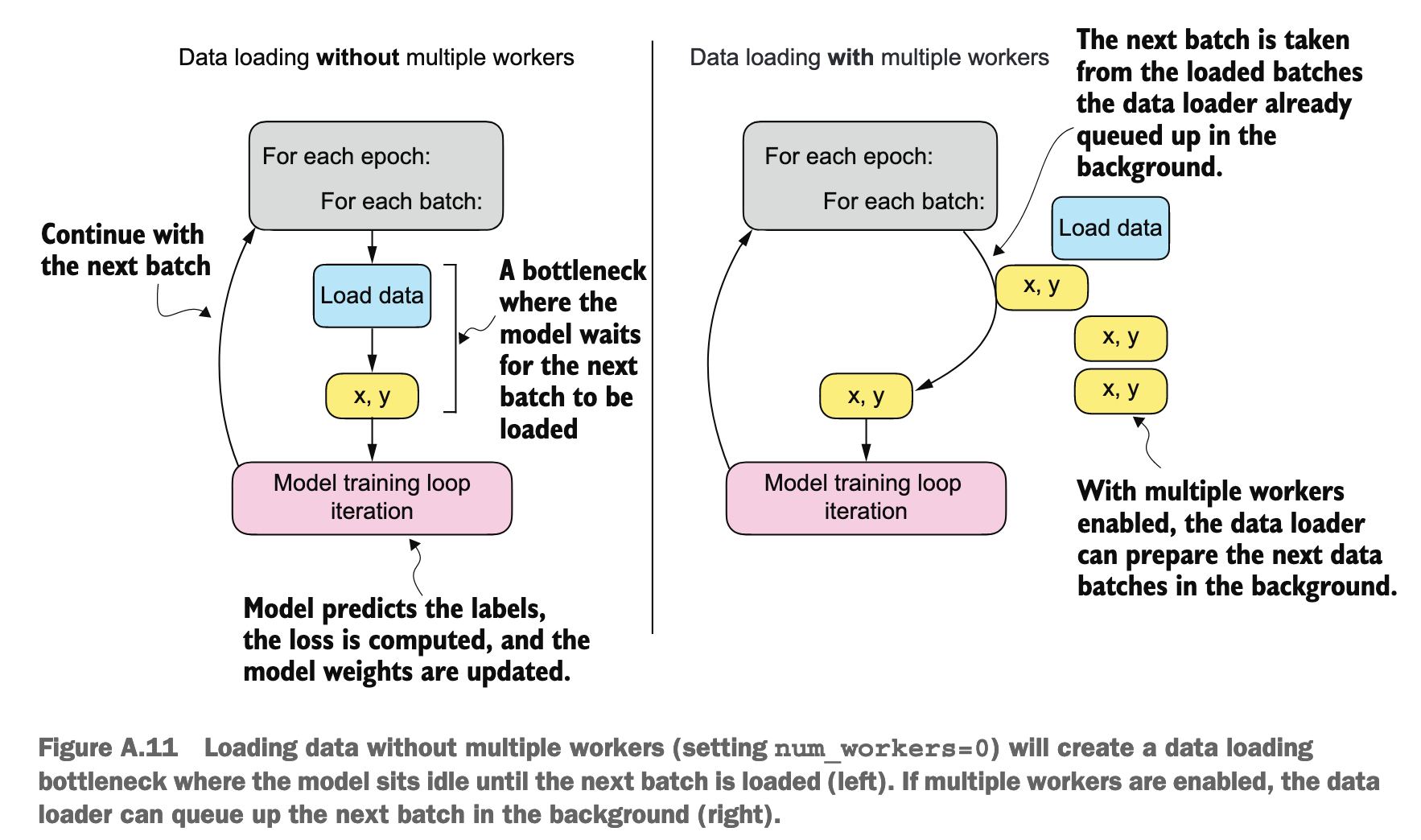
pasted-image-20250521153401.png

Training Loop

import torch.nn.functional as F

torch.manual_seed(123)
model = NeuralNetwork(num_inputs=2, num_outputs=2)
optimizer = torch.optim.SGD(model.parameters(), lr=0.5)

num_epochs = 3

for epoch in range(num_epochs):
    
    model.train()
    for batch_idx, (features, labels) in enumerate(train_loader):

        logits = model(features)
        
        loss = F.cross_entropy(logits, labels) # Loss function
        
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
        ### LOGGING
        print(f"Epoch: {epoch+1:03d}/{num_epochs:03d}"
              f" | Batch {batch_idx:03d}/{len(train_loader):03d}"
              f" | Train/Val Loss: {loss:.2f}")

    model.eval()
    # Optional model evaluation

  • model.train() (设置为训练模式)

    • 作用：此方法告诉模型及其所有子模块（层）它们现在处于“训练模式”。
    • 影响的层：
      • Dropout 层：在训练模式下，Dropout 层会按照设定的概率随机地将一些神经元的输出“丢弃”（置为零），这是一种正则化技术，有助于防止模型过拟合。
      • Batch Normalization (BatchNorm) 层：在训练模式下，BatchNorm 层会计算当前批次数据的均值和方差，并用它们来归一化数据。同时，它还会更新一个在整个训练过程中持续学习的“运行均值 (running mean)”和“运行方差 (running variance)”。
    • 何时使用：在每个 epoch 开始训练数据迭代之前，你应该调用 model.train()，以确保所有对训练敏感的层都以其正确的训练时行为运行。

  • model.eval() (设置为评估模式)

    • 作用：此方法告诉模型及其所有子模块（层）它们现在处于“评估模式”（也常用于推理或测试）。
    • 影响的层：
      • Dropout 层：在评估模式下，Dropout 层会被禁用。这意味着所有的神经元都会被激活（或者说，它们的输出会按照训练时保留的概率进行缩放），模型会使用其完整的学习能力来进行预测，得到一个确定性的输出。
      • Batch Normalization (BatchNorm) 层：在评估模式下，BatchNorm 层不再使用当前批次数据的均值和方差来归一化。相反，它会使用在整个训练过程中学习到的“运行均值”和“运行方差”来进行归一化。这确保了在评估或推理时，模型的输出是确定性的，并且不依赖于当前输入批次的统计特性。
    • 何时使用：当你需要评估模型在验证集或测试集上的性能时，或者在部署模型进行实际预测（推理）之前，都应该调用 model.eval()。在你的代码片段中，它被放在了每个 epoch 训练迭代之后，这通常是准备进行验证或记录模型在固定状态下性能的地方。

Saving and Loading Models

torch.save(model.state_dict(), "model.pth")

model = NeuralNetwork(2, 2) model.load_state_dict(torch.load("model.pth"))