Shape Manipulating
reshape
可以把 NumPy 的 reshape 操作想象成一个先摊平, 再重铺的过程
核心思想: 无论你原来的数组是什么形状,也无论你想要变成什么新形状,reshape 都会(概念上)做两步:
- 摊平 (Flattening): 一行一行地把整个数组中的元素读出来, 形成一维数组
- 重铺 (Refilling): 再根据
reshape后的形状填满一行一行地填满整个数组
import numpy as np
a = np.array([[1, 2, 3, 4, 5, 6], [7, 8, 9, 10, 11, 12]])
# Flatten
a_flat = a.reshape(1, 12)
print("Flattened array: ", a_flat)
# Refill
a_refilled = a_flat.reshape(3, 4)
print("Refilled array: ", a_refilled)
transpose
高维转置的本质是重新安排数组的索引顺序,而不是传统意义上的"矩阵转置"
concatenate & stack
concatenate: 沿着现有的轨道/维度进行延伸或对接
concatenate 是将多个数组沿着一个已经存在的维度(轴,axis)拼接起来。结果数组的维度数量通常与输入数组的维度数量相同
工作方式:
- 你需要指定一个
axis参数,告诉 NumPy 沿着哪个维度进行拼接。 - 除了要拼接的那个维度之外,其他所有维度的大小必须完全相同。 就像你要把两列火车车厢接起来,它们的高度和宽度得匹配,只有长度可以不同(然后加起来)
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6]])
# 注意:B 也是二维的,才能在 axis=0 上与 A 匹配列数 np.concatenate((A, B), axis=0)
# 结果:
# [[1, 2],
# [3, 4],
# [5, 6]] (行数增加了,列数不变)
A = np.array([[1, 2], [3, 4]])
C = np.array([[5, 6], [7, 8]])
np.concatenate((A, C), axis=1)
# 结果:
# [[1, 2, 5, 6],
# [3, 4, 7, 8]] (列数增加了,行数不变)
stack: 将多个独立的层叠放起来,形成一个新的维度
核心思想:
stack是将多个数组沿着一个新的维度组合起来。因此,结果数组的维度会比输入数组的维度多一个工作方式:
- 所有输入数组的形状必须完全相同。 因为它们要成为新维度上的“切片”
- 你需要指定一个
axis参数,这个参数定义了新维度插入的位置
axis=0: 新维度在最前面, 可以理解为相同类型的数据, 增加了一个"批次"的维度
a = np.array([[1, 2], [3, 4]]) # 照片1
b = np.array([[5, 6], [7, 8]]) # 照片2 (必须和 a 形状一样)
stacked_0 = np.stack((a, b), axis=0)
# 结果 (形状: 2x2x2):
# [[[1, 2], <-- a 的内容 (第一张照片)
# [3, 4]],
# [[5, 6], <-- b 的内容 (第二张照片)
# [7, 8]]]
# 新的维度 0 表示照片的索引 (0 代表 a, 1 代表 b)
axis=1: 新维度在中间
stacked_1 = np.stack((a, b), axis=1)
# 结果 (形状: 2x2x2):
# [[[1, 2], <-- a 的第一行
# [5, 6]], <-- b 的第一行 (新维度在它们之间)
# [[3, 4], <-- a 的第二行
# [7, 8]]] <-- b 的第二行
这里,stacked_1[0] 是 [[1,2], [5,6]]。它把 a 的第一行和 b 的第一行沿着新创建的轴(axis=1)堆叠起来了
axis=-1: 新维度在最后, 可以理解为把两个数组按照元素为单位进行堆叠, 对于每个元素, 都增加了一个新的维度来区分它是哪个批次的
stacked_2 = np.stack((a, b), axis=2) # 或者 axis=-1
# 结果 (形状: 2x2x2):
# [[[1, 5], <-- a[0,0] 和 b[0,0] 堆叠
# [2, 6]], <-- a[0,1] 和 b[0,1] 堆叠
# [[3, 7], <-- a[1,0] 和 b[1,0] 堆叠
# [4, 8]]] <-- a[1,1] 和 b[1,1] 堆叠
concatenate vs stack 总结
| 特性 | concatenate (连接) | stack (堆叠) |
|---|---|---|
| 维度变化 | 结果维度数通常不变 (除非输入是一维) | 结果维度数 +1 |
| 操作轴 | 沿着现有的轴进行拼接 | 沿着新创建的轴进行堆叠 |
| 输入形状 | 在非拼接轴上形状需一致,拼接轴上可不同 | 所有输入数组形状必须完全相同 |
| 思维模型 | “延伸”、“对接”、“粘合” | “叠放”、“分层”、“增加厚度/深度” |
axis含义 | 指定哪个现有的轴作为拼接方向 | 指定新轴插入的位置 |
- 当你想要把数据块扩展现有维度时,比如把更多的行加到表格底部,或者把更多的列加到表格右边,用
concatenate - 当你有一系列相同形状的“样本”或“层”,你想把它们组织成一个更高维度的数据结构,其中新增的维度代表样本索引或层索引时,用
stack
broadcasting
广播的机制就像是 NumPy 自动地把较小的数组“拉伸(复制)”它的值,直到它的形状与较大数组的形状兼容,然后再执行元素对元素的操作
核心思想: 尽可能地让维度匹配,如果某个维度的大小是 1,就认为它可以“扩展”到另一个数组在该维度上的大小
广播的规则(Rules of Broadcasting)
NumPy 广播遵循一套严格的规则来确定两个数组是否兼容:
规则 1:对齐维度 如果两个数组的维度数量不同,那么较小维度数组的形状会在其左边(前面)补 1,直到两个数组的维度数量相同。
规则 2:维度兼容性检查与“拉伸” 从最末尾的维度开始,逐个比较两个数组对应维度的大小:
- a) 完全匹配: 如果两个维度的大小相同,则这个维度是兼容的。
- b) 其中一个为 1: 如果其中一个数组在该维度上的大小是 1,那么这个维度也是兼容的。NumPy 会(概念上)“拉伸”这个大小为 1 的维度,使其匹配另一个数组在该维度上的大小(可以理解复制, 直到把这维填满)
- c) 不匹配且均不为 1: 如果两个维度的大小不同,并且没有任何一个是 1,那么这两个数组是不兼容的,NumPy 会抛出
ValueError
规则 3:操作执行 如果两个数组根据上述规则是兼容的,NumPy 就可以执行元素对元素的操作。结果数组的形状将是两个输入数组在各个维度上尺寸的最大值
标量与数组相加
import numpy as np
a = np.array([1, 2, 3, 4])
b = 5
result = a + b
print(f"a: {a}, shape: {a.shape}")
print(f"b: {b} (scalar)")
print(f"result: {result}, shape: {result.shape}")
- 标量
b(值为5) 会被“拉伸”或“复制”4次,变成概念上的[5, 5, 5, 5]
一维数组与二维数组相加 (行广播):
M = np.array([[1, 2, 3],
[4, 5, 6],
[7, 8, 9]]) # shape (3, 3)
v = np.array([10, 20, 30]) # shape (3,)
result = M + v
print(f"M:\n{M}, shape: {M.shape}")
print(f"v: {v}, shape: {v.shape}")
print(f"result:\n{result}, shape: {result.shape}")
- 对齐维度:
v变为 (1,3):[[10,20,30]] - 拉伸: 把内层的
[10,20,30]复制两次
更复杂的类型:
x = np.arange(4).reshape(4, 1) # shape (4, 1) -> [[0],[1],[2],[3]]
y = np.arange(3).reshape(1, 3) # shape (1, 3) -> [[0,1,2]]
result = x + y
print(f"x:\n{x}, shape: {x.shape}")
print(f"y:\n{y}, shape: {y.shape}")
print(f"result:\n{result}, shape: {result.shape}")
- 都变为
(4, 3)
x 变为:
[[0, 0, 0],
[1, 1, 1],
[2, 2, 2],
[3, 3, 3]] # 形状 (4, 3)
y 变为:
[[0, 1, 2],
[0, 1, 2],
[0, 1, 2],
[0, 1, 2]] # 形状 (4, 3)
A three-dimensional array would be like a set of tables, perhaps stacked as though they were printed on separate pages
二维数组可以认为是 a set of arrays, 即第一维存放的是索引, 不是真实的数据
如果 “真实的"数据是二维的话, 那么 四维数组 可以看做是一个"二维数据容器”
It is familiar practice in mathematics to refer to elements of a matrix by the row index first and the column index second. This happens to be true for two-dimensional arrays, but a better mental model is to think of the column index as coming last and the row index as second to last. This generalizes to arrays with any number of dimensions.
常用的 array attributes:
ndimshapesizedtype
Create arrays:
np.zeros(2)np.ones(2)np.empty(2)- random values, speed first
np.arrange(2)- you can specify the first number, last number, and the step size
While the default data type is floating point (np.float64), you can explicitly specify which data type you want using the dtype keyword
x = np.ones(2, dtype=np.int64)
To add elements:
a = np.array([1, 2, 3, 4])
b = np.array([5, 6, 7, 8])
np.concatenate((a, b))
You may want to take a section of your array or specific array elements to use in further analysis or additional operations.
a = np.array([[1 , 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
# five_up is a bool array
five_up = (a >= 5)
print(a[five_up])
a = np.array([[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]])
five_up_condition = (a >= 5)
a_filtered_shape_preserved = np.where(five_up_condition, a, 0)
To get indices rather than value:
b = np.nonzero(a < 5)
print(b)
list_of_coordinates= list(zip(b[0], b[1]))
a1 = np.array([[1, 1],
[2, 2]])
a2 = np.array([[3, 3],
[4, 4]])
np.vstack((a1, a2))
array([[1, 1],
[2, 2],
[3, 3],
[4, 4]])
np.hstack((a1, a2))
array([[1, 1, 3, 3],
[2, 2, 4, 4]])
vstack在 axis 0 上进行堆叠 (row)- 如果数组
a1的形状是(d1, r1, c1),数组a2的形状是(d2, r2, c2), 结果数组的形状将是(d1 + d2, r1, c1)
- 如果数组
hstack在 axis 1 上进行堆叠 (col)- 如果数组
a1的形状是(d1, r1, c1),数组a2的形状是(d2, r2, c2), 结果数组的形状将是(d1, r1 + r2, c1)
- 如果数组
对 arrays 进行 slice 操作创建的是 view, 共享底层内存
Basic array operations
在 numpy 中, array 的加减乘除是逐元素操作的
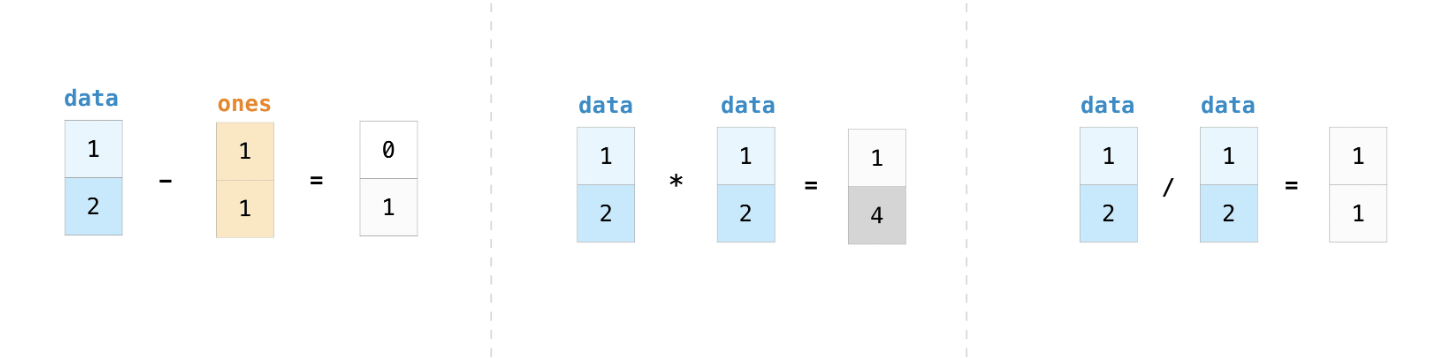
Matrix
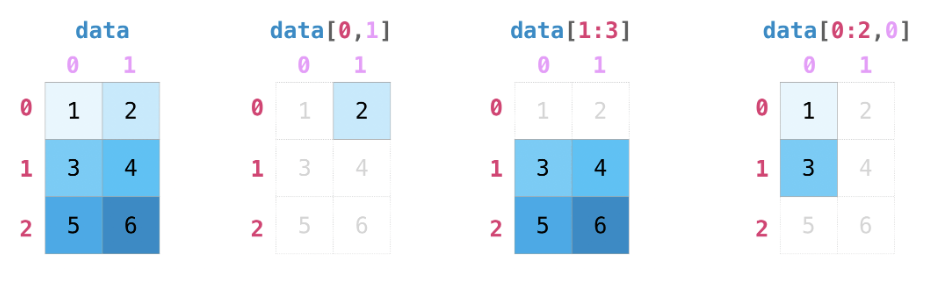
data = np.array([[1, 2], [3, 4], [5, 6]])
data[0, 1]
2
data[1:3]
array([[3, 4],
[5, 6]])
data[0:2, 0]
array([1, 3])
data.max(axis=0)
array([5, 6])
>>> data.max(axis=1)
array([2, 5, 6])
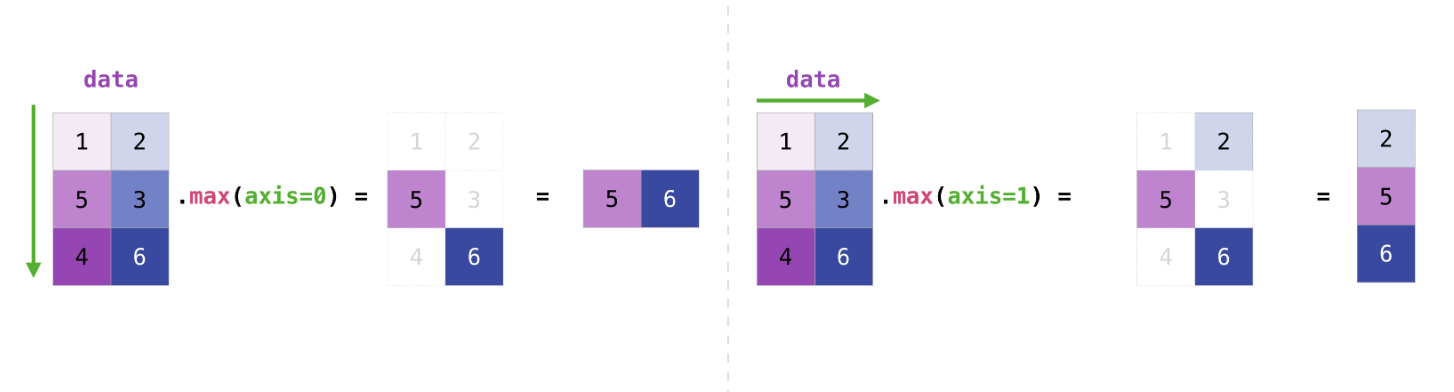
axis=0就是沿着 row 变化的方向遍历, 收集最值 (也就是收集 colunm 的最值)
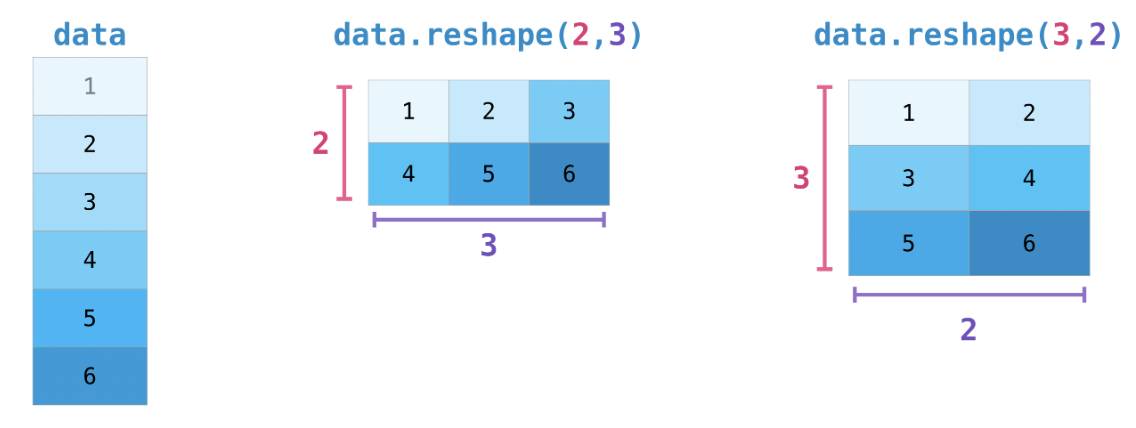
Transposing and reshaping a matrix
data = np.array([1,2,3,4,5,6])
print(data.reshape(2, 3))
print(data.reshape(3, 2))
You can transpose your array with arr.transpose()
arr = np.arange(6).reshape((2, 3)).transpose()
arr = np.arange(6).reshape((2, 3)).T
Matrix Multiple
当你在 NumPy 中处理三维或更高维的数组,它并非简单地将所有元素相乘,而是遵循一套清晰的“堆叠矩阵”和广播规则。
核心机制:关注最后两维,广播其余维度
“矩阵”的定义:对于高维数组,NumPy 将最后两个维度视为传统意义上的矩阵的行和列。例如,一个形状为
(b, n, m)的数组被看作是b个n x m的矩阵堆叠在一起。执行乘法:矩阵乘法主要作用于这两个“矩阵”维度。对于两个数组
A和B,如果要计算C = A @ B:A的形状为(..., n, m)B的形状应该为(..., m, k)C的形状为(..., n, k)
处理“批处理”维度:最后两维之外的其他前导维度被视为“批处理”或“堆叠”维度。NumPy 会在这些维度上应用广播规则:
- 如果前导维度的形状不完全相同但兼容广播(例如,其中一个数组的某个维度大小为 1,或者一个数组的前导维度比另一个少),NumPy 会自动扩展(广播)维度较小的数组,使其与维度较大的数组匹配,然后再执行上述的“批处理”矩阵乘法。
广播的例子
如果 arr1 的形状是 (3, 4) (一个单独的 3x4 矩阵),而 arr2 的形状是 (2, 4, 5) (2 个 4x5 矩阵)。
执行 result = arr1 @ arr2:
- NumPy 会将
arr1(形状(3,4)) 广播到arr2的批处理维度上。它会认为arr1需要与arr2中的 每一个4x5矩阵相乘。 arr1 @ arr2[0]会计算出来。arr1 @ arr2[1]也会计算出来。- 结果
result的形状将是(2, 3, 5)。