Extensive Reading
Author Info
Background
While speculative decoding improves latency by using a smaller draft model to generate tokens for a larger target model, it suffers from two specific bottlenecks:
- Autoregressive Drafting: The draft model itself generates tokens autoregressively (one by one), which is still computationally expensive and slow.
- Inefficient Time Allocation: Standard methods allocate equal time to generate every draft token. However, tokens later in the sequence have a significantly lower probability of acceptance. Using the same computational resources for these “high-rejection” tokens is inefficient.
Insights
- The autoregressive process of draft model is the bottleneck: Use draft model to accelerate draft models (Vertical Cascade)
- Tokens later in the sequence have a lower probability of acceptance: Use a faster and lighter draft model later in the sequence (Horizontal Cascade)
Challenges
Approaches
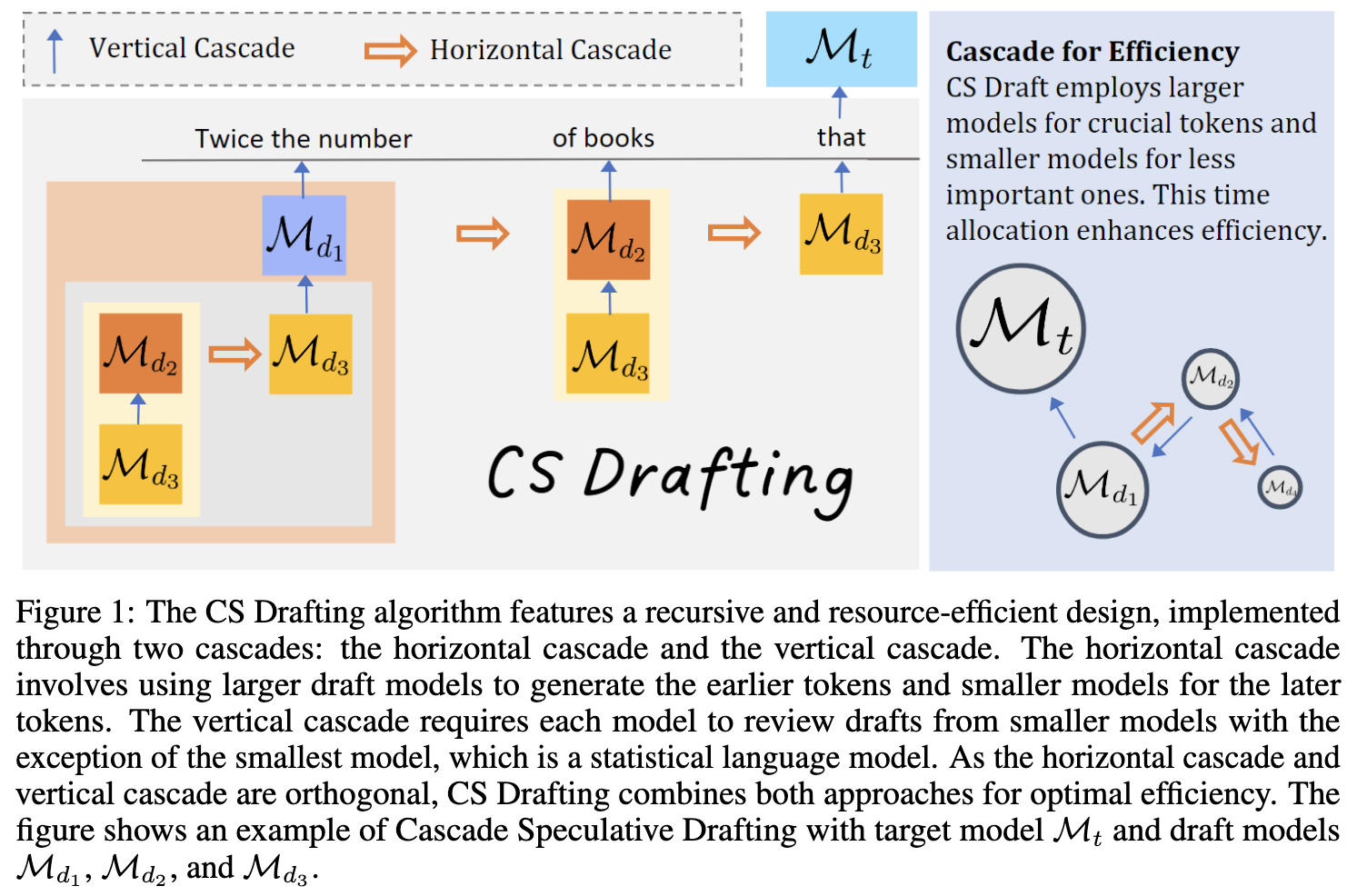
Vertical Cascade
Recursive Drafting
A smaller model generates a draft for the current draft model. This eliminates the autoregressive generation step for the neural draft model, turning it into a “reviewer” rather than a “generator.”
- This process is recursive: Model $\mathcal{M}_{d_2}$ reviews the output of $\mathcal{M}_{d_3}$, and $\mathcal{M}_{d_1}$ reviews $\mathcal{M}_{d_2}$.
As long as the draft model can be accelerated, the original speculative process can be accelerated, too.
Horizontal Cascade
Positional Allocation
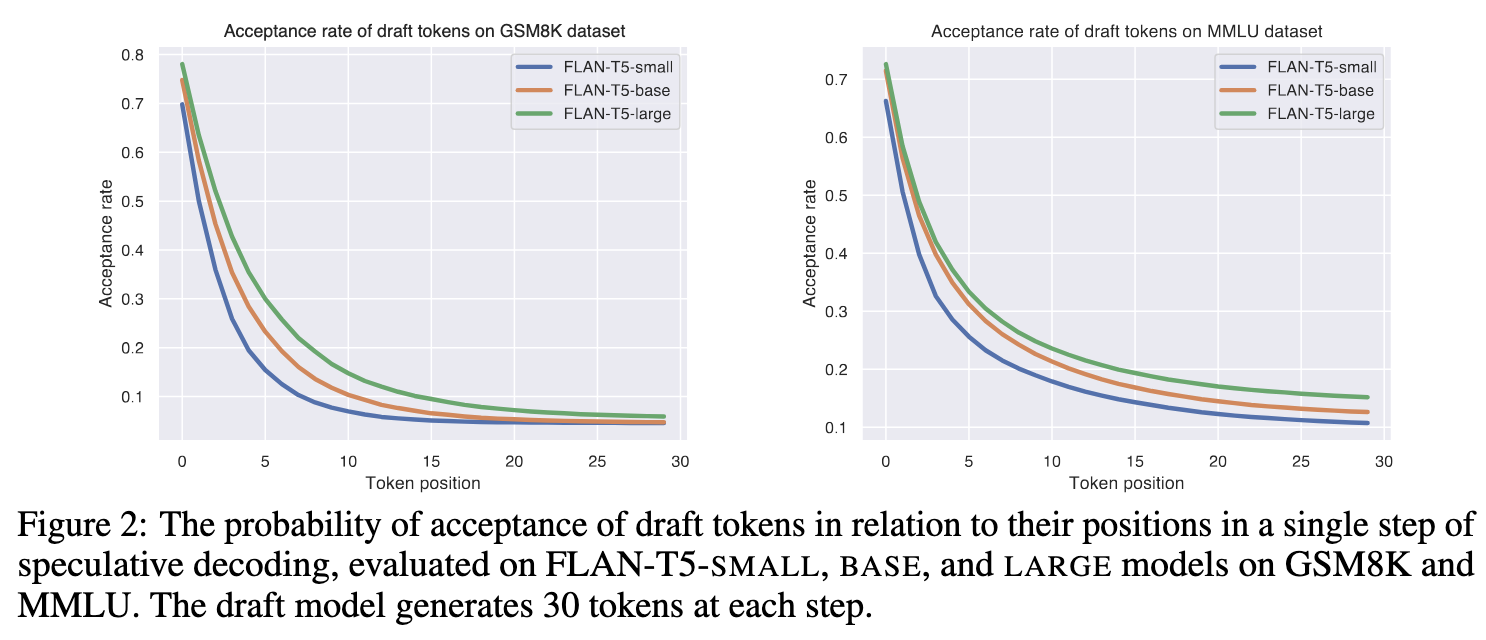
The probability of a token being accepted by the target model decreases exponentially with its position in the sequence.
So horizontal cascade assigns larger, more accurate draft models to generate earlier tokens and smaller, faster models to generate later tokens.
- Prevent wasting expensive computational resources on late-position tokens that are highly likely to be rejected.
Max-Gram
PLD?
n-gram 是基于统计的概率预测,而 Max-Gram 是基于上下文的“复制粘贴”机制
n-gram (统计语言模型):
- 原理: 基于马尔可夫假设,认为下一个词的出现概率只依赖于前面 $n-1$ 个词。
- 预测方式: 它在一个预先计算好的概率表中查找当前 prefix 最可能接续的词。例如,在 Bigram (n=2) 中,它根据当前词 $w_i$ 查找概率最高的 $w_{i+1}$。
- 静态的概率查表过程 Max-Gram (MaG):
- 原理: 基于“文本局部重复性”的假设。它认为在当前的 prompt 或已生成的文本中,很多短语是会重复出现的。
- 预测方式: 它在 Context Window 中进行搜索。它寻找与当前句尾(Suffix)匹配的最长子串。一旦找到这个最长的匹配片段,它就直接查看该片段在之前出现时后面紧跟的是什么词,并将该词作为预测结果。
- 动态的字符串匹配与复制过程
- n-gram 依赖于外部通用语料库(如维基百科、Common Crawl 等)训练得出的统计分布。它反映的是语言的全局规律,与当前特定文档的内容无关。
- Max-Gram 依赖于当前推理时的局部上下文, 利用的是当前文档内部的特定信息。
Analyzing
Expected acceptance rate $\alpha(\mathcal{M}_t, \mathcal{M}_d)$ is the probability of draft generation by $\mathcal{M}_d$ being accepted by target model $\mathcal{M}_t$.
Cost coefficient $c(\mathcal{M}_t, \mathcal{M}_d)$ is the ratio of time for a single run of draft model $\mathcal{M}_d$ over target model $\mathcal{M}_t$.
Expected walltime improvement factor (EWIF): is the expected time improvement achieved by an algorithm under the i.i.d. assumption of token acceptance.
$$\text{EWIF} = \frac{\text{Target Model 接受的平均 token 数}}{\text{生成这些 token 所花费的归一化时间成本}}$$分母比较简单,计算的是完成一轮推测所需的总计算量(以 Target Model 运行一次的时间为单位 1):
$$(1+nc_{d_{1}}+nkc_{d_{2}})$$分子:
$$\frac{1-\alpha\phi^{n}(\alpha)}{1-\alpha}$$计算的是:在这一轮中,Target Model 预期能接受多少个 token,$\phi(\alpha)$ 为 草稿长度的概率生成函数在接受率 $\alpha$ 处的取值
最后的公式是
$$\text{EWIF} = \frac{1-\alpha\phi^{n}(\alpha)}{(1-\alpha)(1+nc_{d_{1}}+nkc_{d_{2}})}$$如果模型足够快,且有正向的收益,EWIF 就会提升,以 MaG 模型举例
- MaG 速度足够快 $c_{d_2} << 1$, 分母几乎不变
- 只要 MaG 能偶尔才对一些词,$\phi(\alpha)$ 就会体现出正值。这会使得分子(预期接受的 token 数)增加
分母(成本)几乎不变,分子(收益)增加 $\rightarrow$ EWIF 提升
这段数学推导严格证明了:只要最底层的 Draft Model 足够快(成本可忽略),哪怕它很笨,把它加进系统里也稳赚不赔。
Evaluation
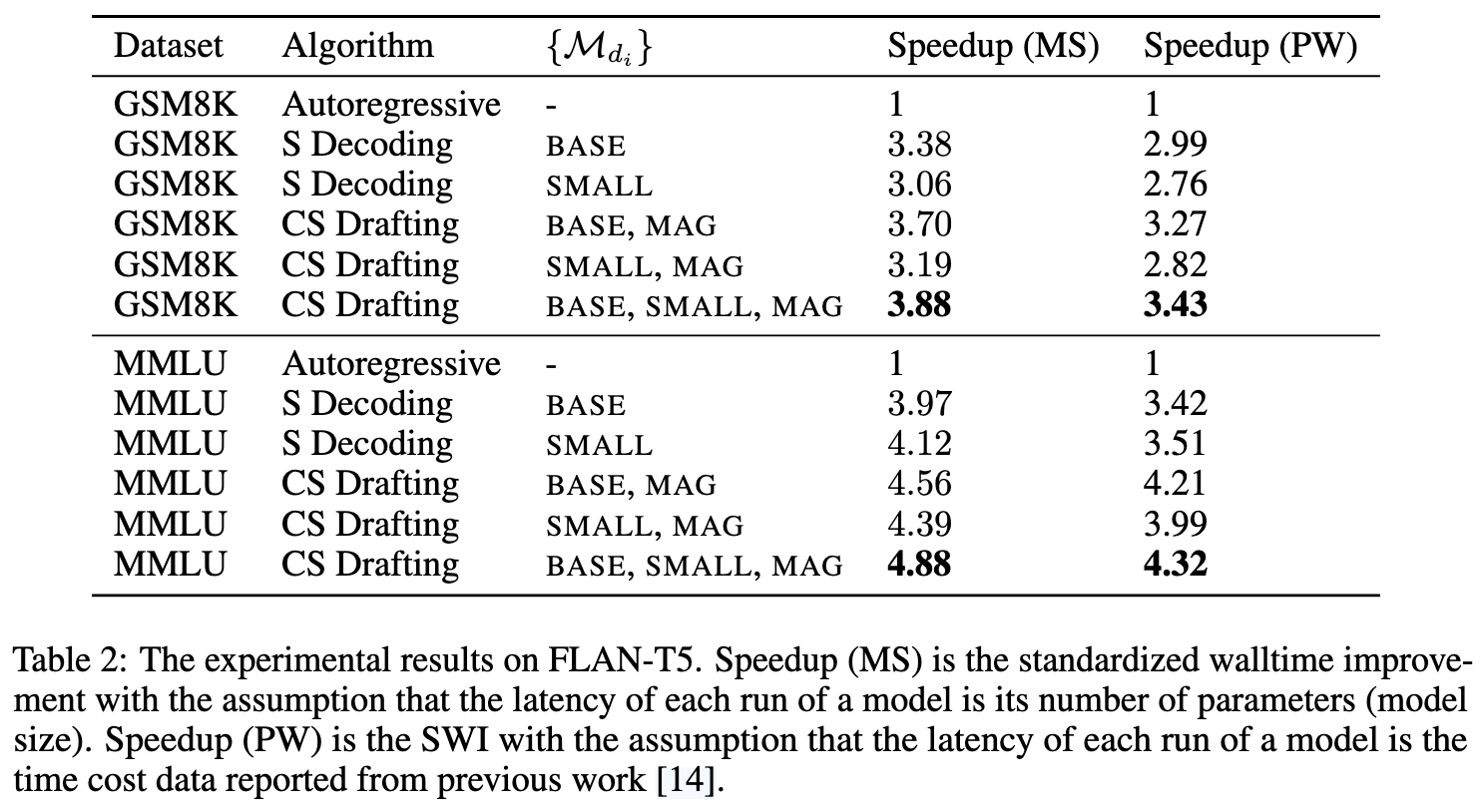
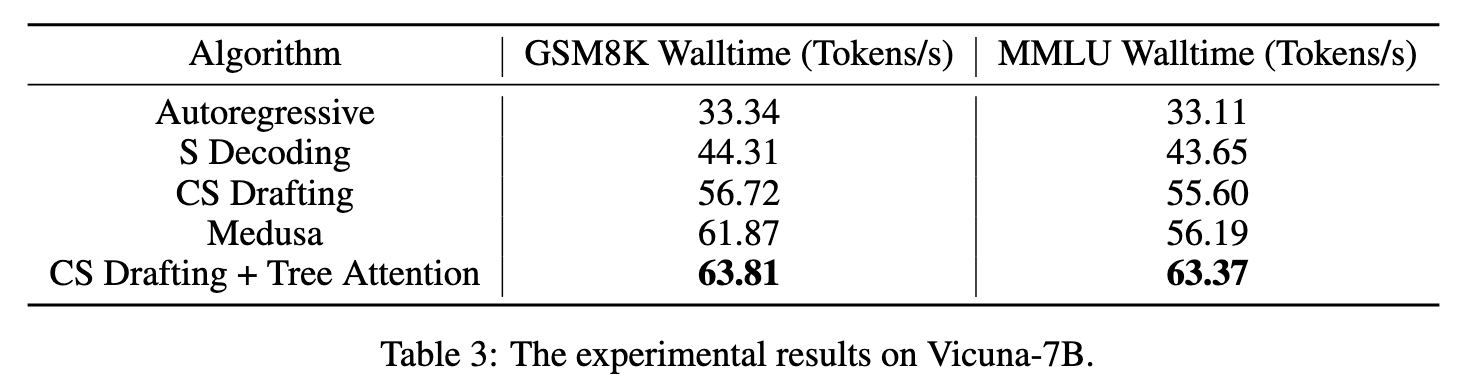
Thoughts
When Reading
Related Works
Implementation
import random
class Model:
def __init__(self, name):
self.name = name
def generate(self, prefix, max_len=1):
"""模拟生成:Base Case (如 MaG) 直接生成"""
return [f"{self.name}_token"]
def review(self, prefix, draft, lenience=1):
"""模拟审核:Target Review"""
# 简单模拟:假设以一定概率接受
# 论文中 lenience (l) 用于放宽中间层的审核标准
accepted = []
for token in draft:
if random.random() < 0.8: # 模拟接受率
accepted.append(token)
else:
break # 拒绝,截断
return accepted
def cascade_speculative_drafting_step(draft_models, target_model, prefix, K_matrix, l_lenience):
"""
对应论文 Algorithm 1: CascadeSpeculativeDraftingStep
"""
# --- Base Case (递归终止条件) ---
# 对应论文: if draftList is empty then ...
# 当没有更小的草稿模型可用时,当前的最底层模型(target_model, 即 MaG)直接生成
if not draft_models:
# 这里模拟 MaG 的非自回归生成或简单生成
return target_model.generate(prefix)
# 初始化
cur_gen = [] # 对应 curGen (相对于 prefix 的增量)
full_prefix = prefix[:] # 保持当前完整的上下文
# 获取当前层级的 horizontal 步长配置
# 对应论文: [k1, ..., kn-1] <- first row of Knn
current_level_ks = K_matrix[0]
# --- Horizontal Cascade Loop (水平级联循环) ---
# 对应论文: for i <- 1 to n do ...
# 这个循环体现了"水平级联":随着 i 增加,负责审核的 target 变小(draft_models[i])
for i, k_i in enumerate(current_level_ks):
# 1. 确定当前的"临时目标"和"临时助手列表"
# 对应论文: curTarget <- draftList[i]
cur_target = draft_models[i]
# 对应论文: curDraftList <- sublist of draftList starting from i+1
cur_draft_list = draft_models[i+1:]
# 对应论文: curK <- submatrix of Knn ...
# (简化处理:切片取剩余的配置)
cur_K = [row[i+1:] for row in K_matrix[1:]]
# 2. 生成当前片段 (Segment Generation)
# 对应论文: while curGen.length ... < ki do
# 只要当前片段还没凑够 k_i 个词,就持续递归调用
segment_len = 0
while segment_len < k_i:
# --- Vertical Cascade (垂直级联递归) ---
# 对应论文: Recursive Call -> CascadeSpeculativeDraftingStep
# 这里的关键是:用更小的模型列表 (cur_draft_list) 为当前模型 (cur_target) 生成草稿
sub_draft = cascade_speculative_drafting_step(
cur_draft_list,
cur_target,
full_prefix + cur_gen,
cur_K,
l_lenience
)
cur_gen.extend(sub_draft)
segment_len += len(sub_draft)
# (为了防止无限循环的模拟保护)
if len(sub_draft) == 0: break
# --- Final Review (最终审核) ---
# 对应论文: review(Mt, curGen, ...)
# 所有的片段拼凑好后,由本层原本的 target_model 进行统一度量
# 注意:论文提到如果是最顶层调用,l=1;中间层调用 l>1 (Lenience)
accepted_draft = target_model.review(prefix, cur_gen, lenience=l_lenience)
return accepted_draft
# ==========================================
# 模拟运行
# ==========================================
# 定义模型层级: Target -> Draft1 -> Draft2 -> MaG
# 实际传入函数的 draft_models 列表是 [Draft1, Draft2, MaG]
target_mt = Model("Target(LLaMA-70B)")
draft_1 = Model("Draft1(LLaMA-7B)")
draft_2 = Model("Draft2(Tiny)")
mag = Model("MaG(N-gram)")
draft_list = [draft_1, draft_2, mag]
# 定义 K 矩阵 (简化版)
# K_matrix[0] 控制最顶层 Horizontal 分配:
# - 位置 0 (交给 Draft1 负责): 目标生成 3 个词
# - 位置 1 (交给 Draft2 负责): 目标生成 2 个词
# - 位置 2 (交给 MaG 负责): 目标生成 1 个词
# Row 0 ([3, 2, 1]): 决定了最终输出序列是由谁拼凑的。(一段 Draft1 的,一段 Draft2 的,一段 MaG 的)。
# Row 1 ([2, 1]): 决定了 Draft 1 是如何被加速的。
# Row 2 ([1]): 决定了 Draft 2 是如何被加速的。
K_matrix = [
[3, 2, 1],
[2, 1], # 下一层的配置
[1] # 再下一层的配置
]
print("Running Algo 1 (Cascade Speculative Drafting)...")
final_result = cascade_speculative_drafting_step(
draft_models=draft_list,
target_model=target_mt,
prefix=["The", "future"],
K_matrix=K_matrix,
l_lenience=1
)
print(f"Final Accepted Draft: {final_result}")