Extensive Reading
Author Info
Prerequisite
贝叶斯优化是一种用于全局优化的策略,专门用于解决黑盒函数(Black-box function)的极值问题。它特别适用于那些评估代价昂贵(computationally expensive)、不可导或没有解析表达式的复杂函数。
其核心思想是:不要盲目地搜索,而是根据已有的历史数据构建一个概率模型,智能地推测下一次应该尝试哪里,从而以最少的尝试次数找到全局最优解。
贝叶斯优化由两个关键部分组成:
- 代理模型(Surrogate Model):
- 这是对目标函数的一种概率近似。最常用的是高斯过程(Gaussian Process, GP)。
- 与普通回归模型不同,代理模型不仅预测某个输入点对应的函数值(均值),还会给出一个不确定性范围(方差)。
- 作用:它告诉我们“根据目前已知的点,目标函数长什么样”以及“我们在哪些地方比较确信,哪些地方完全不知道”。
- 采集函数(Acquisition Function):
- 这是根据代理模型来指导下一步决策的函数。常见的有 Expected Improvement (EI) 或 Upper Confidence Bound (UCB)。
- 它负责解决探索(Exploration)与开发(Exploitation)的权衡问题:
- Exploitation:去代理模型预测值最好的地方,试图找到当前的局部最优。
- Exploration:去代理模型不确定性最高(方差大)的地方,试图发现未知的潜在最优解。
- 作用:它计算搜索空间中每个点的“潜在价值”,价值最高点就是下一次实验的参数。
- 观察:根据当前的初始数据点,训练代理模型(高斯过程)。
- 决策:最大化采集函数,找到下一个最有希望的候选点 $x$。
- 评估:在真实的复杂系统(目标函数)中运行这个参数 $x$,得到真实结果 $y$。
- 更新:将新的数据对 $(x, y)$ 加入历史数据,更新代理模型的后验概率分布。
- 重复:重复上述步骤,直到达到预定的迭代次数或满足收敛条件。
凡是符合**“输入参数维度不高(通常<20维)”且“验证一次结果很慢或很贵”**的问题,都是贝叶斯优化的用武之地
Background
Standard autoregressive decoding is slow because it generates tokens sequentially, and each step is memory bandwidth-bound.
Self-Speculative Decoding speeds up inference by generating “draft” tokens quickly using a simplified version of the model and then verifying them in parallel using the full model. Unlike traditional speculative decoding, which requires a separate, smaller “draft model,” this approach derives the draft model directly from the original LLM by skipping layers.
Insights
- Skipping certain layers in LLMs does not significantly compromise the generation quality.
- By selectively bypassing some intermediate layers, we can use the LLM itself to generate draft tokens.
到这里整篇论文的思路就基本清晰了,只需要关注下面几点:
- Skipping layers 如何选择?动态还是静态?
- 最后生成的 Draft Model 生成速度相比完整的模型快了多少?
Challenges
- It is non-trivial to determine which layers and the number of layers to skip during drafting.
- It is hard to decide when to stop the generation of draft tokens.
第二个挑战其实就是一个常见的 Adaptive Threshold
Approaches
The paper formulates this as an optimization problem to minimize the average inference time per token.
Bayesian Optimization (BO) is employed offline to search for the optimal combination of layers to skip. It uses a Gaussian process to model the objective function and balances exploration and exploitation to find the best configuration.
目标函数为 $f(z)$,$z$ 是一个向量,表示每一层是否应该跳过
$$f(z) = \frac{\text{Drafting Time}(z) + \text{Verification Time}}{\text{Average Accepted Tokens}(z) + 1}$$优化问题是这么描述的:
$$ \mathbf{z}^* = \arg \min_{\mathbf{z}} f(\mathbf{z}), \quad s.t. \ \mathbf{z} \in \{0, 1\}^L. $$arg min 的意思是 “使目标函数达到最小值的那个参数”
所以把选择 Skipping Layer 的问题建模为了贝叶斯优化问题:
- 代理模型为高斯过程
- 采集函数没有特别说明,可能是常见几种中的某一种
确定模型之后,离线跑多轮迭代,最后对于一个模型,确定一个固定的 Skipping Layer 集合
只看方法部分可能觉得是直接跳过某个完整 layer, 也就是 attn + MLP,但是实验结果确实以单个 Module 为单位的:
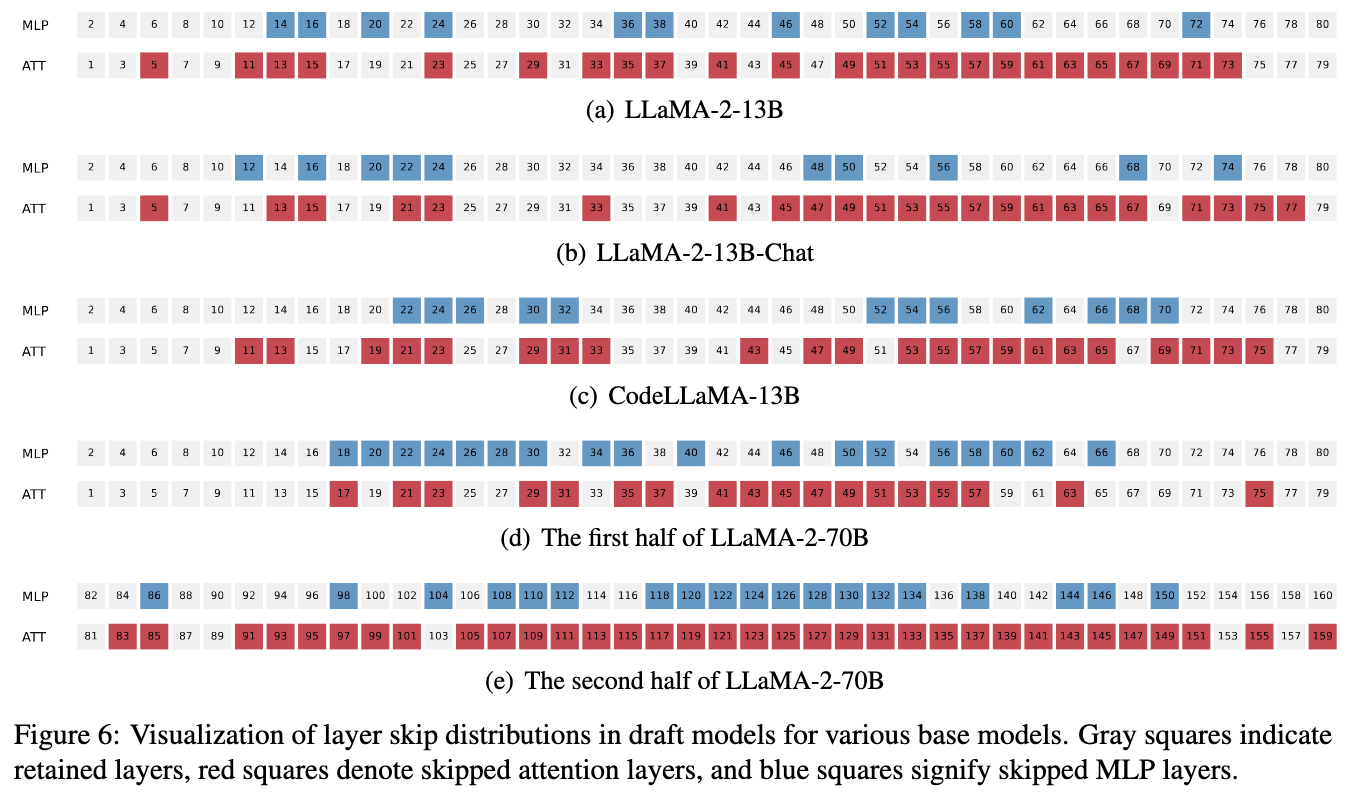
至于 Adaptive Threshold:
def update_adaptive_threshold(self, batch_acceptance_rate):
"""
根据论文公式 (2)-(4) 更新自适应阈值 gamma
"""
# 更新移动平均接受率 AR
self.current_ar = self.alpha * self.current_ar + (1 - self.alpha) * batch_acceptance_rate
# 更新阈值 gamma
if self.current_ar <= self.target_ar:
# 接受率太低,提高门槛,少生成点垃圾草稿
self.gamma = self.gamma + 0.02
else:
# 接受率很高,降低门槛,多生成点草稿
self.gamma = self.gamma - 0.02
# 限制 gamma 范围
self.gamma = max(0.0, min(1.0, self.gamma))
Evaluation
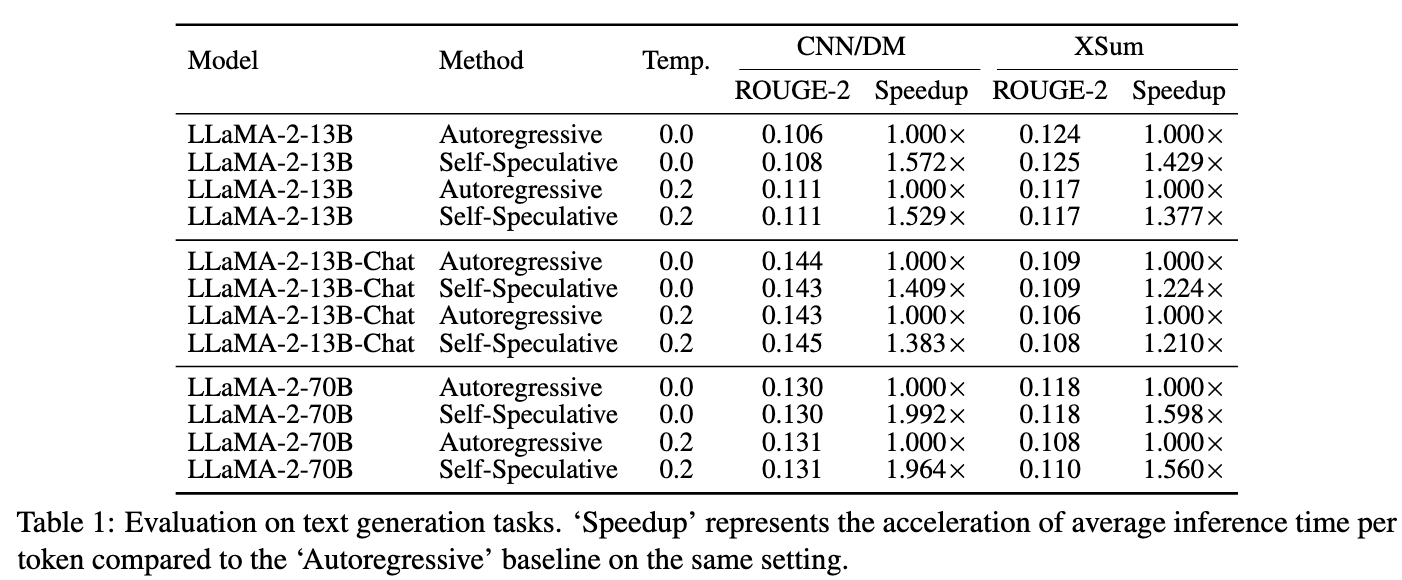
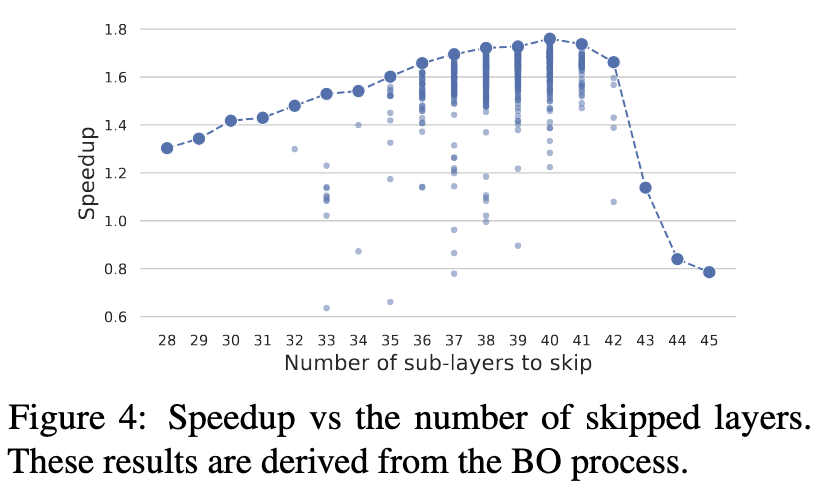
- Figure 4 uses LLaMA-2-13B, which comprises 80 layers
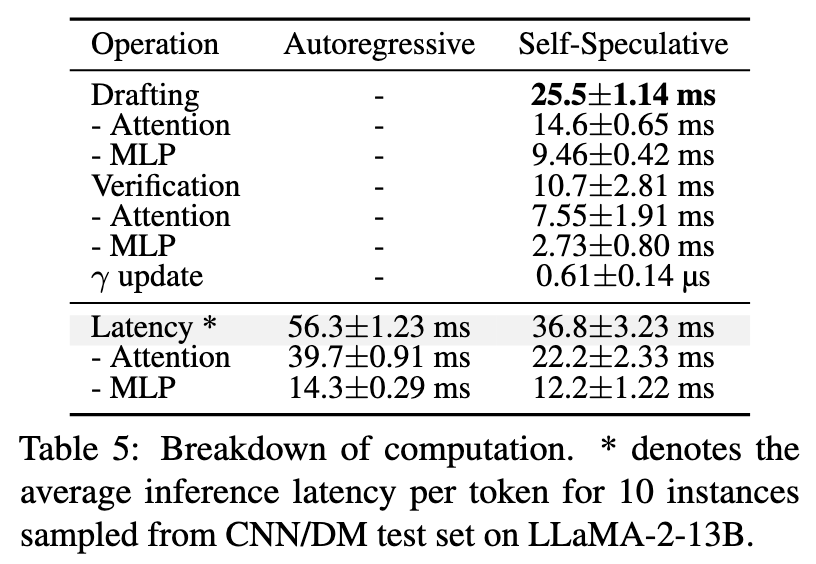
注意这里统计的是 “latency per token”
所以可以得到以下数据:
- Full model forward: 56.3ms
- Draft model forward: 25.5ms
- 根据 Figure 6, LLaMA-2-13B 跳过了 34 层,也就是 0.425
- 0.425 * 56.3 = 23.9,和 Draft model 差不多
Thoughts
When Reading
使用贝叶斯优化来确定哪些 Layer 可以跳过比较有意思
但其实还能更"语义化一点",根据 CAS-Spec Cascade Adaptive Self-Speculative Decoding for On-the-Fly Lossless Inference Acceleration of LLMs, 其他技术还能继续放在其中继续增强
根据实验数据,LLaMA-2-13B 减掉了 34 层来作为 Draft model, 那我直接使用一个同系列的 5B 模型呢,谁的效果更好?